
希望杯模拟试卷 4 下载 Word模板 爱问共享资料
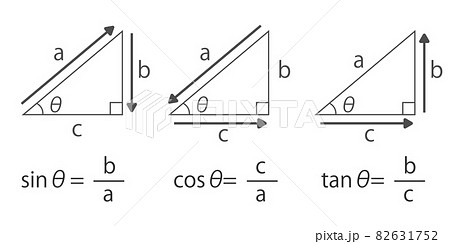
使用本三角形在线计算器 ,它可以计算直角三角形及斜角三角形的任意答案,输入3个条件即可求出另外的边长及和面积,三角形求角度。 关于我们 网站帮助 广告合作 网站声明 友情连接 网站地图・ 直角三角形 (底辺と角度) 直角三角形の底辺と角度から、高さと斜辺と面積を計算します。 ・ 直角三角形 (高さと斜辺) 直角三角形の高さと斜辺から、底辺と角度と面積を計算します。 ・ 直角三角形 (高さと角度) 直角三角形の高さと角度から、底辺と斜辺と面積を計算します。 ・ 直角三角形 (斜辺と角度) 直角三角形の斜辺と角度から、底辺と高さと面積を計算します。 三角関数 ・ 角度から三角
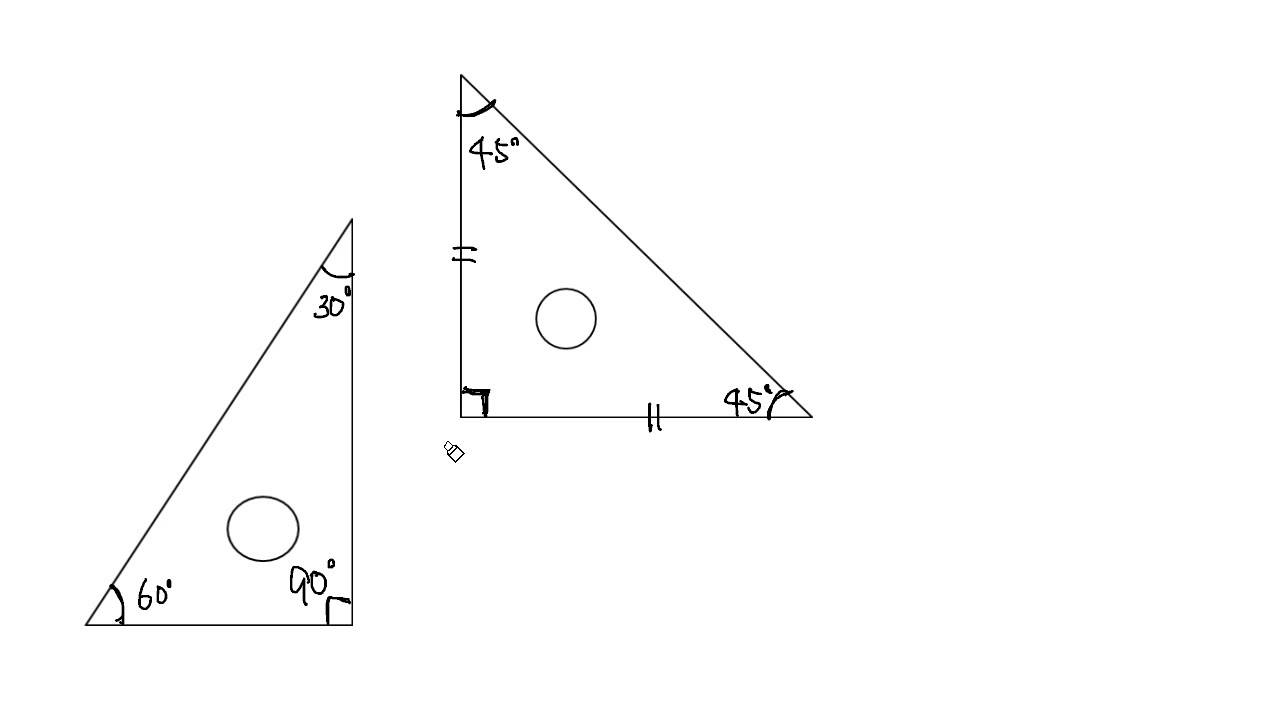
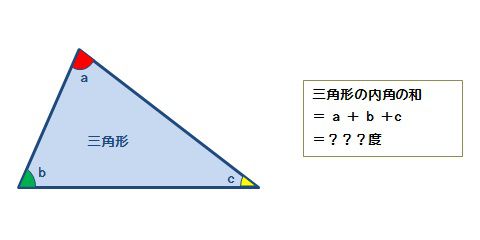
三角形 角度 合計
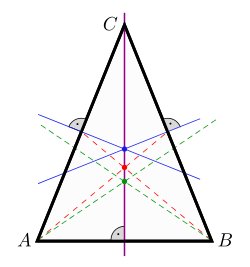
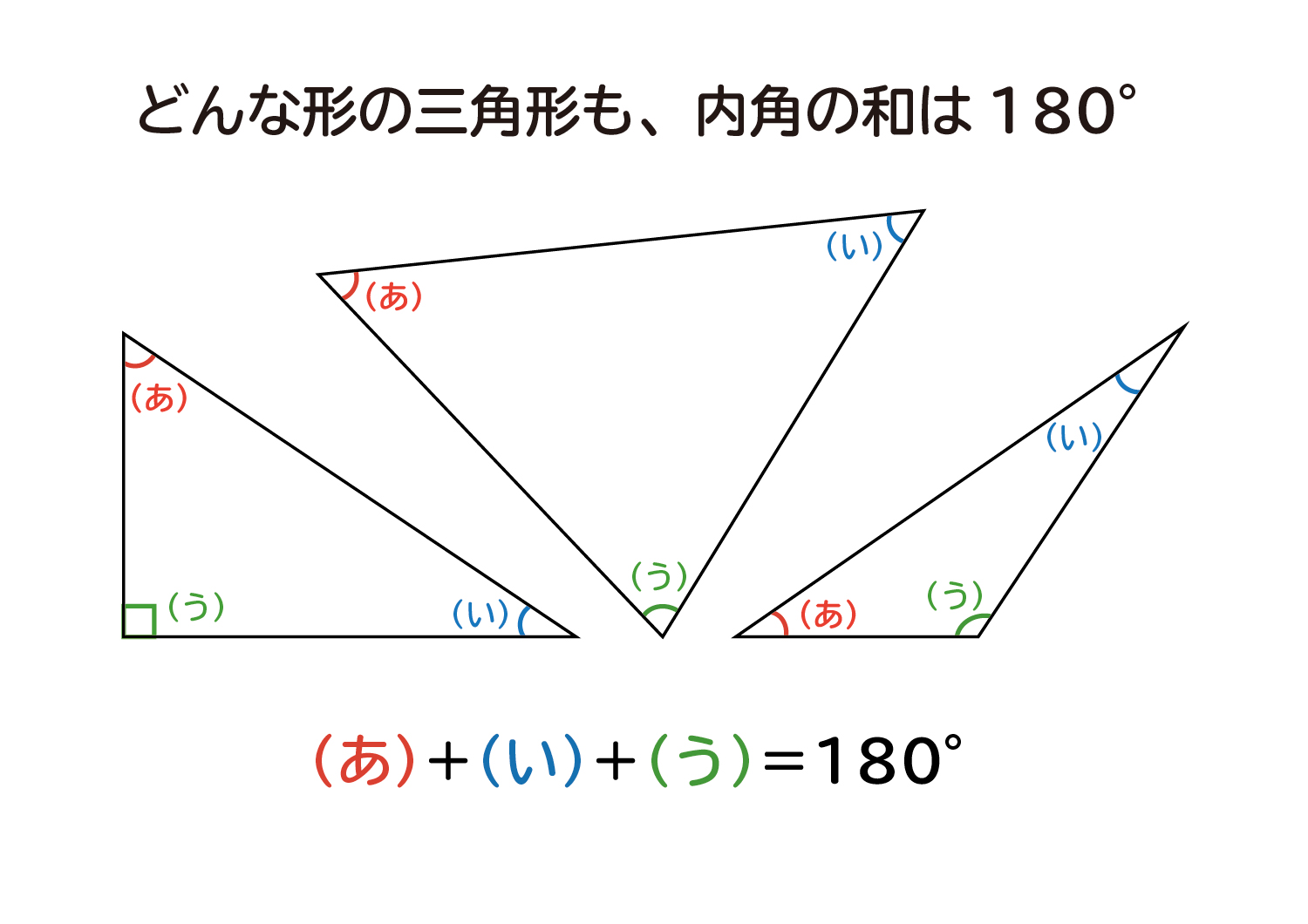
三角形 角度 合計- 五角形の中に三角形が3つも潜んでいるから なんだ。 まず、 対角線を2本ひいてみよう。 すると、どうだろう?? 三角形が3つも隠れていることがわかるよね。 三角形の内角の和は「180°」で、5角形には三角形が3つもかくれているんだ。 よって、三角形にはいろんな種類があり、形や大きさは様々です。 しかしどんな三角形でも、 「3 3 つの角の内角をすべて足すと絶対に180° 180 ° になる」 という定理があります。 「図の a a の角度を求めよ」というような問題が出された場合にこれを用います。 内角の和 (a 125°23°) ( a 125 ° 23 ° ) が 180° 180 ° なので、 180− 125−23=32 180 − 125 − 23 = 32 となり、 a a は 32° 32 ° と求め
一个高速发展的医疗细分行业 腾讯新闻
多角形の基本の形は三角形です。 四角形は三角形が2つ 五角形は三角形が3つ 六角形は三角形が4つ ・・・ と増えていくだけです。 なので多角形の内角の和は三角形の数に関係しています。 三角形の内角の和は\(\,180°\,\) これは忘れたら角度は求まりません。多角形の内角の角度の合計を見つける 角度の合計を求めるには、 (n – 2) x 180という計算式を用います。 ここでの「n」とは多角形を構成する辺の数を意味しています。 また、最も一般的な多角形の角度の合計は下記の様になっています。 三角形(3辺から 三角形は、平面上で3つの点とこれらの点を対で結ぶ3つの線分で囲まれた最も単純な多角形です。 三角形の角度は鋭い、鈍いそしてまっすぐです。 三角形の角度の合計は一定で180度です。 あなたが必要になります 幾何学と三角法に関する基礎知識;
角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。細長い三角形もきれいな三角形も180度ですが、もう一度、なぜ三角形の角度の合計が180度なのか、分かるように教えてください。 私 >直角三角形の3つの角度と一辺(対辺)の長さが分かっている時、隣辺の長さを求める方法は? 水色の三角形は二等辺三角形だから底角は等しい。 よって、底角のxは、 (180-1)÷2=30 になるぞ。 円周角の問題9 円周角115°だから、赤い中心角は2倍の230°。 紫のとこは、 360-230=130° だから、求めるxは、 180-130=50° うんうん。 みるからに50°だ。
三角形 角度 合計のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  |  |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  | |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | ||
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「三角形 角度 合計」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |
二等辺三角形の両底角は等しい. が成り立ちます. この性質と三角形の内角の和が 180 °になるという性質を使うと,二等辺三角形の3つの角のうち1つの角が分かれば,残りの角が求められます. 例1 頂角が与えられている問題 が成り立ちますユークリッド空間、和三角形の角度は等しい直角度(180度、 π ラジアン、2つの直角、又は半ターン)。 三角形は、 3つの角度、それぞれに1つずつ有している頂点の隣接の対によって囲まれ、側面を。 この合計が異なる他の形状が存在するかどうかは、長い間知られていませんでした。
Incoming Term: 三角形 角度 合計 証明, 三角形 角度 合計,




0 件のコメント:
コメントを投稿