上 二次関数 y=x2乗 グラフ 295457-二次関数 y=x2乗 グラフ

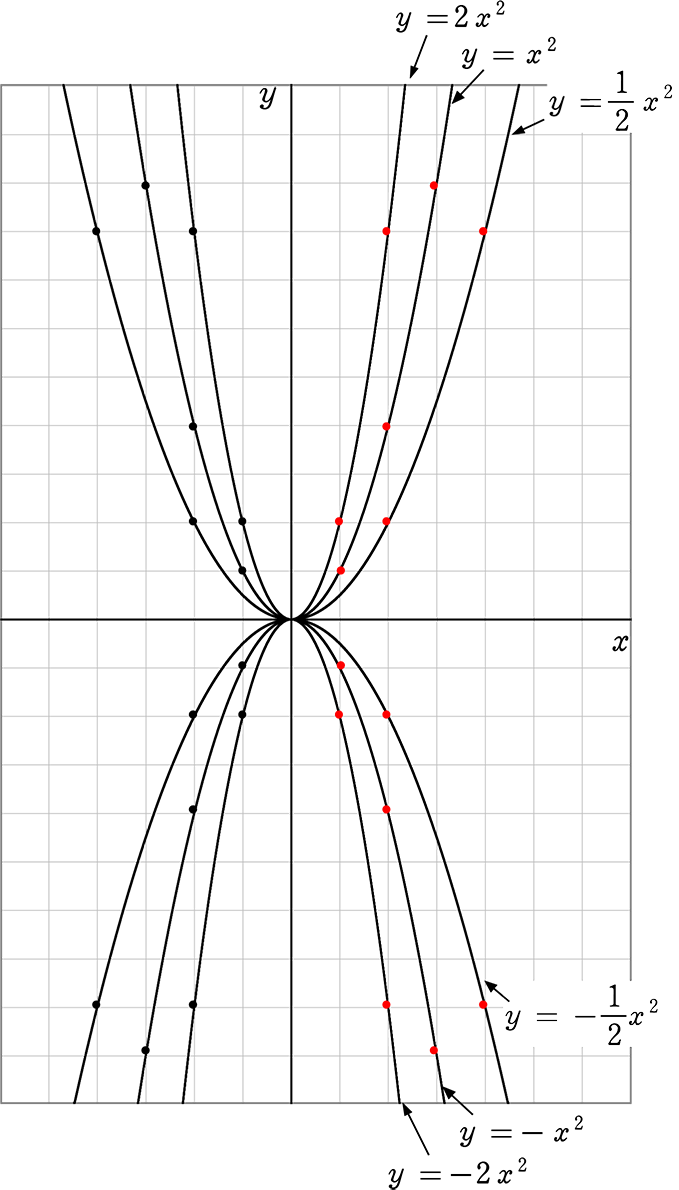
中3／2次関数 → 携帯版は別頁 ≪解説≫ y＝x 2 ，y＝2x 2 ，y＝3x 2 などのようにy＝ax 2 の形で書かれる関数を， yが xの2乗に比例する関数 といいます． 例 y＝2x 2 の場合，2x 2 の計算は x 2 を先に計算し ，その結果に2を掛けます． x＝1ならばy＝2× 1 2 ＝2× 1Y=x2乗－2x－2を平方完成したらどうなりますか？ 途中式教えてください 詳説数学Ⅰ第二章 2次関数（前半）～関数とグラフ～ 「二次関数の理解」を最大値まで完璧にするノート3選二次関数のグラフを平行移動したいときは 移動後のグラフの頂点の座標を求め、 y = a ( x p) 2 q に代入する。 このやり方は実はあまり効率がよくない上に、二次関数でしか使えないので、ぜひ「別解」の方もマスターしてください。 別解として、 平行

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

二次関数 y=x2乗 グラフ

二次関数 y=x2乗 グラフ-質問＜2818＞あいか「2次関数」 y=x^212x13のグラフを平行移動して y=x^24x5のグラフに重ねるには どのように平行移動すればよいか。 質問＜2785＞HY「二次関数の決定」 次の条件を満たす放物線の方程式を求めよ。2乗に比例する関数のグラフは直線ではないため、 できるだけたくさんの点をとりフリーハンドでなめらかな曲線のグラフをかく。 y= 1 4 x 2 のグラフの書き方 xの値を式に代入して下の表を埋める。 → x 8 6 4 2 0

2次関数のグラフ 2次関数のグラフの式の 頂点の求め方を教えて下さい Okwave

1．指数関数ってなに？ 指数部分にx(変数)がある関数のことを言います。 ↓こんなグラフになります！ そうです、数学Ⅱ（高校二年生レベル）で学習します！ 意外と単純なグラフですネ♪ xが2倍、3倍になると、 yは4倍、8倍になります。 2．指数関数的増加 y = a x y 2 = a x y=\sqrt{ax}\iff y^2=ax y = a x y 2 = a x かつ y ≥ 0 y\geq 0 y ≥ 0 なので，グラフは放物線の一部になります（よく見る y = x 2 y=x^2 y = x 2 という放物線を 9 0 ∘ 90^{\circ} 9 0 ∘ 回転させたものの半分）。 b ≠ 0 b\neq 0 b = 0 の場合は平行移動すればよいだけです。 例えば、y=x 24x10という二次関数のグラフを、x軸方向に3、y軸方向に5平行移動させる場合を考えてみます。 平行移動の解き方：その1 1つ目解き方は、平方完成を利用する方法です。 まずは平行移動させたい二次関数を平方完成します。

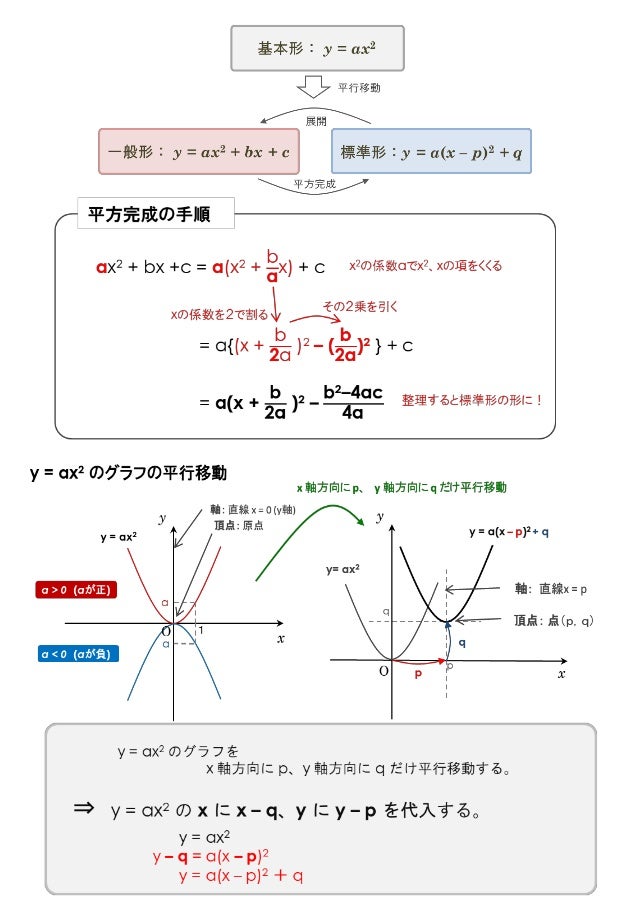
このとき，点Pの座標は(a, b)であるといい，値aのことを点Pのx座標，値bのことを 点Pのy 座標という．またP(a, b)のように表す． 3（いよいよ）グラフについて 関数の性質を視覚的（図形的）に理解するためにグラフを用いる． 定義 yをxの関数とするとき，xの各々値に対しyの値が唯一つに定まる 二次関数y=a (xp)^2のグラフ 例として、 y = x2 y = x 2 のグラフを x 軸方向に 1 1 だけ移動したものを考えてみます。 グラフは次のようになります。 グレーが移動前、黒い太線が移動後のグラフです。 各点の移動に注目して、グラフを見ながら点の座標をいくY = f (x) y = f ( x) のグラフを、 x x 軸方向に p p y y 軸方向に q q 平行移動すると、 y− q = f (x− p) y − q = f ( x − p) になる。 これは、 2 2 次関数以外のあらゆる関数に成り立つことです。 今後も様々なところで出会うことになるでしょう。 なぜこれが

中3数学。2乗に比例する関数 (y ＝ ax²)。この a は「変化の割合」？ xの値が「0から2まで」増加する？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ 2次関数のコツ、成績アップ法を公開。関数y=ax2乗放物線グラフの書き方はこれでバッチリ！ yはxの2乗に比例する関数 変化の割合二次関数y＝ax2の裏ワザ公式？関数 1変数の関数を，平面上で曲線としてグラフにする． 1変数の関数をプロットする： x^3 6x^2 4x 12のグラフを作成 sin t cos (√3 t)のグラフ プロット 4/ (9*x^ (1/4)) 変数の明示的な変域を指定する： e^x，x=0から10，プロット 実数値の関数をプロット

中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

二次関数のグラフと解の存在範囲の問題をわかりやすく解説

 1．何を学ぶのか中学校で，xの2乗に比例する関数 y=ax2について学習しました。高校ではこの式の右辺がより一般的な2次式となります。つまり，y=ax2bxc という関数を扱うことになります。これを2次関数と呼んでいます。 2次関数のグつまり， 1次関数y＝ax＋bのグラフとx軸の共有点のx座標は，1次方程式ax＋b＝0の解である ，といえるのです。 x軸の共有点では・・・≫ これは，2次関数のときも同様です。 y＝x 2 −4x＋3のグラフとx軸の共有点の座標は， （x，0）とおけるので，y＝x 2 − 4x 発展問題もアリ！ ｜中学数学・理科の学習まとめサイト！ y=ax2乗aの求め方についてパターン別に解説！ 発展問題もアリ！ を求めろって言われても 何をすればいいの！ ？ というわけで、今回の記事では中3で学習する関数 の単元から「 の求め

二次関数のグラフ 二次不等式 戻る 頂点が原点 0 0 の二次関数グラフは中学3年で学習しました 思い出してください下のグラフは２次関数 つまり は の２乗に比例するグラフ Y Ax2で表します 仮に比例定数 ２として Y 2x2のグラフを書いてみま

中３ ２次関数

 2次関数y＝(x＋2)2乗－3の最大値、最小値を教えて下さい。y＝(x＋2)2乗＋1 (－4≦x≦－1) グラフを書き最大値、最小値を教えて下さい。二次関数 y=(x2)²3 は、グラフに書くと 下に凸な放物線になる事は 分かりますか。x の 取り得る範グラフの概形を考えてみてください。 最大値x=0で0 最小値なし ゲスト 1年以上前 ありがとうございます ゲスト 1年以上前 y＝x2乗＋5やy＝－ (x－2)2乗など、平方完成できない式の最大値と最小値の求め方を教えてください この回答にコメントする このY=f(x)= x 3 による逆像。 立方根 3 √の定義 ※一般化：べき関数y=x n によ る逆像

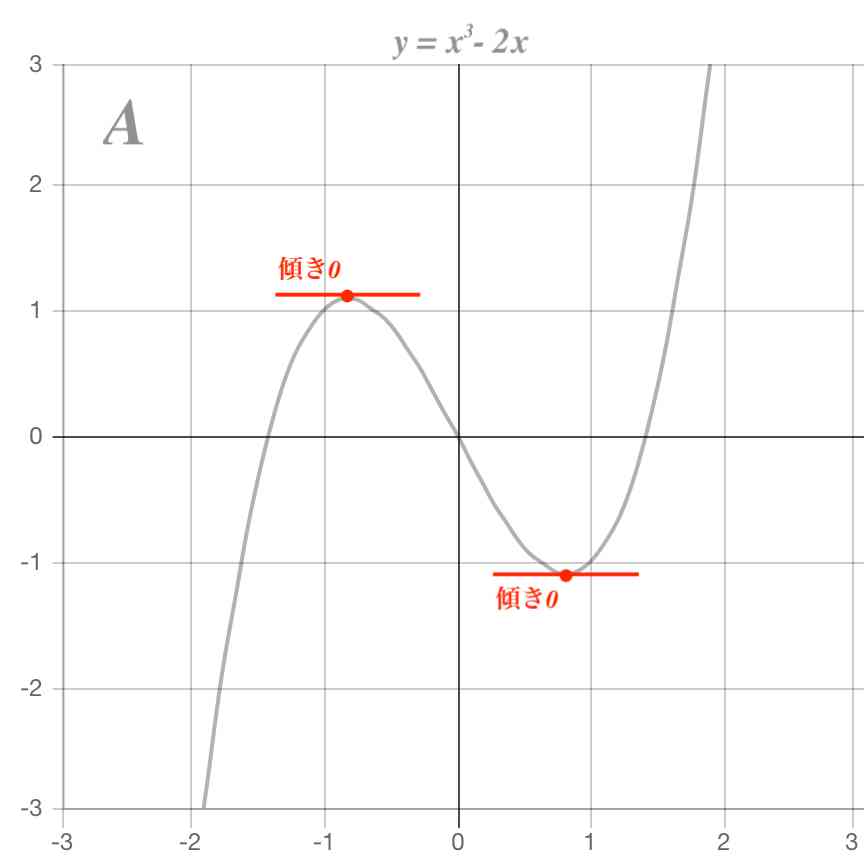
三次関数のグラフの書き方

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

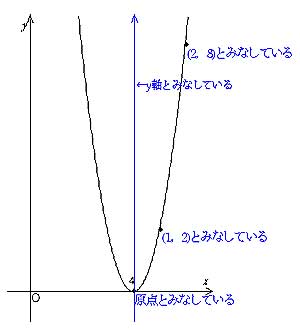
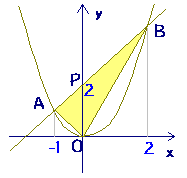
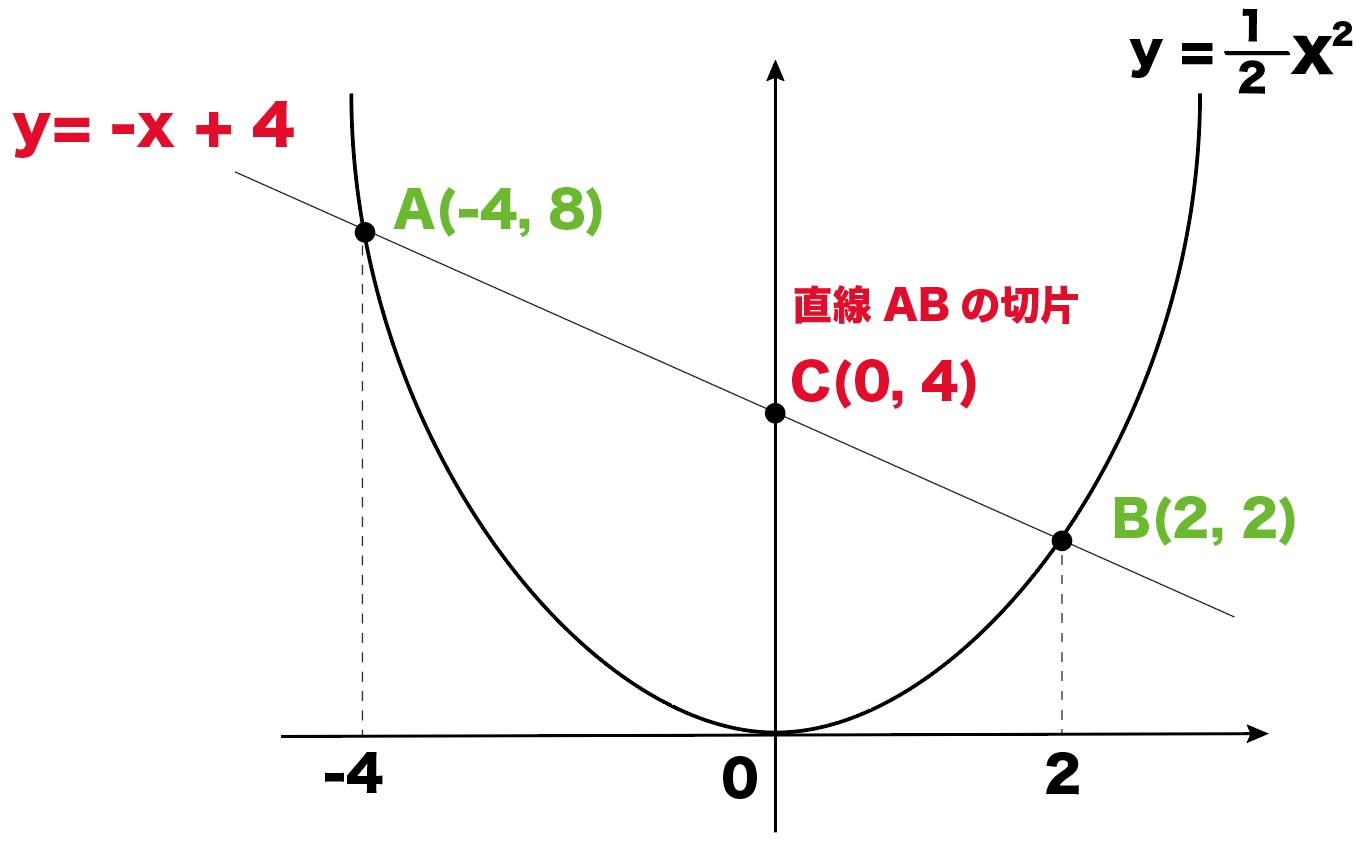
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru y=ax2乗のグラフを書く手順 表を作る 座標を読み取って、グラフに書き込む 点をなめらかな線で結ぶ 完成！ かず先生 では、この手順に従ってグラフを書いてみましょう。 次のグラフを書きなさい。 まずは、表を作ってみましょう。2次関数 y＝x2 のグラフと直線 y＝x＋2 とが交わっているとき，2交点A，Bと原点Oでできる OABの面積の求め方を考えてみます． S1＝2×2÷2＝2です． S2＝2×1÷2＝1です． S＝S1＋S2＝ 3 です． （ OPAの高さは ＋2 です．） 《 問題1 》 次の空欄を埋めなさい

例題で学ぶ高校数学 Y Ax2 Q

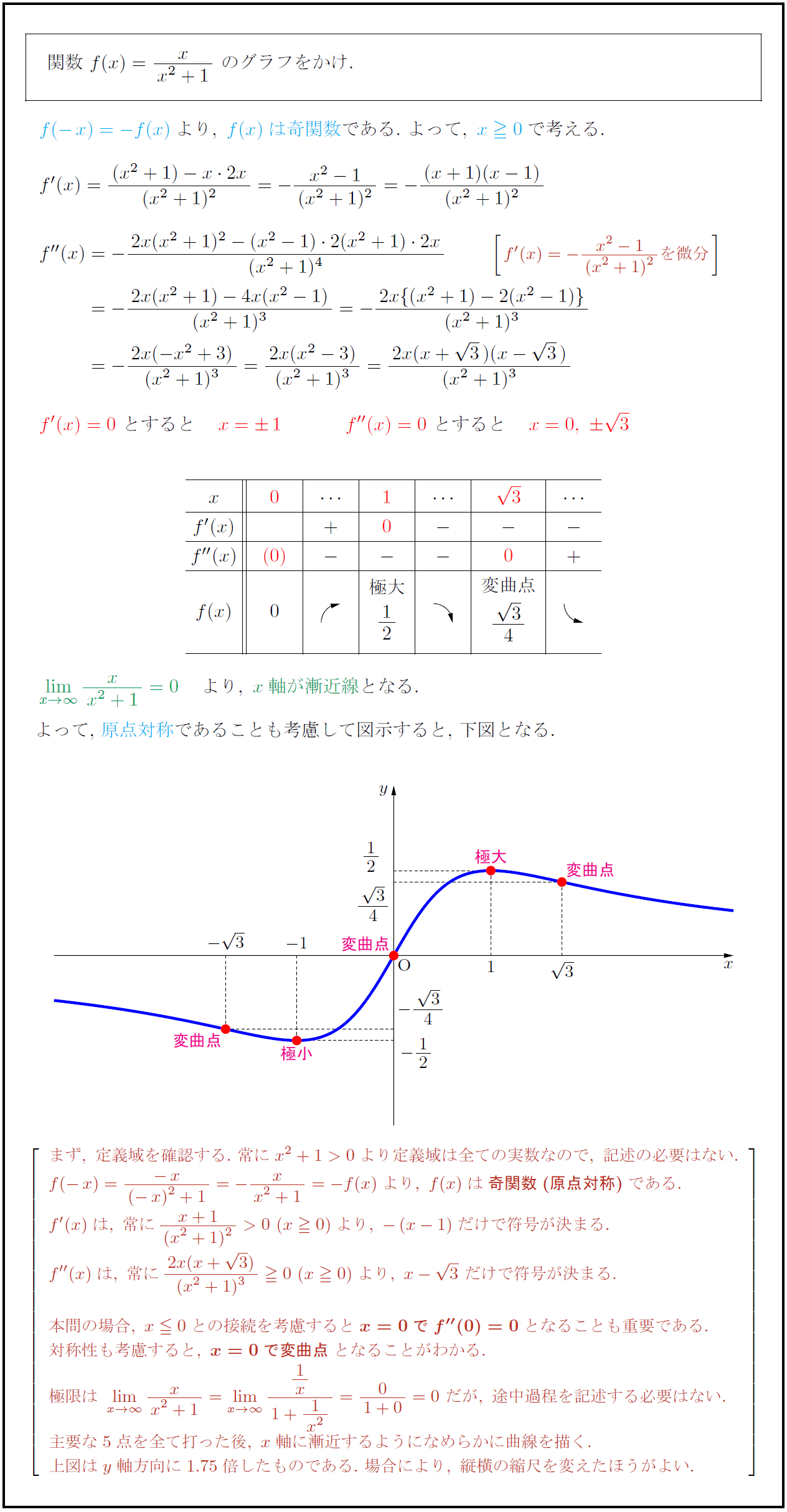
高校数学 分数関数 Y X X 1 のグラフ 受験の月

1．2次関数（2次方程式）y=x 2 のグラフの説明 今回は、2次関数（方程式）のグラフについて考えてみます。 2次関数とは、未知数の一番大きい次数が2になっている関数の式のことをいいます。 次数とは、x 2 を例にすると、エックスの2乗という何乗の部分の2次関数のグラフと x 軸が共有する点，つまり，下の赤い点を 「共有点」 といいます。 この「共有点」の個数で，位置関係を表現すると， という同様の3つのパタ−ンになります。 ≪実数の解の個数に着目≫ 2次関数を y ＝ a x2 ＋ b x ＋ c とすると x 軸は二乗に比例（ひれい）とはy=ax 2 のように「yの値がxの2乗に比例する」ことを言います。 また、単に比例というとy=axのような式のことです。なお「y=ax 2 b」は比例関係では無いので注意しましょう。 比例とは、ある値が2倍、3倍と増える時、もう一方の値も同様の比率で増える関係をいいます。

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

とまて週報 二次関数で語れ１

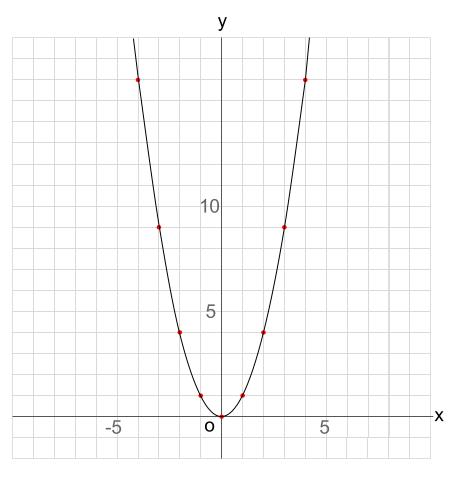
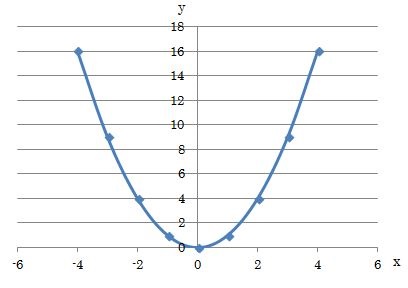
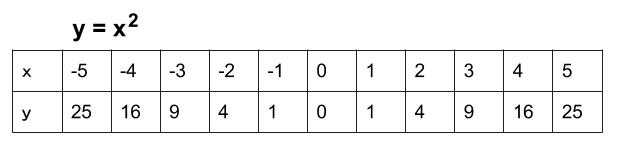
中3数学。2乗に比例する関数（y ＝ ax²）の「変域」を求めなさい。うわ、変域って何？ 頂点が最小？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グイグイ成績が上がる数学のコツ。無料サイトだ。2 2次関数の最も簡単な関数は y =x2 y = x 2 である．この関数についてグラフを考える． x x の値3，2，1，0，1，2，3に対する y y の値をを下の表に示す． 各 x x ， y y の組に対応する点を座標平面に描くと左下の図のようになる．表のような y = x2 y = x 2 の2次関数のグラフを描くWindows Excel13版 セルA1からセルB8の範囲をドラッグして選択します 挿入タブ → グラフグループ → 散布図 → 平滑線とマーカ を選択 y = x 2のグラフができました x = 1 のとき y = 1 (12) になっています

2 裏業

二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

まず、`y = x^2 2x 1` という二次関数を見てみましょう。 この式は、因数分解するだけで `y =(x 1)^2` と2乗の形になっています。 ラッキーですね。 では次に、`y = x^2 2x` という二次関数を見Y＝ax2乗のグラフ書き方 まとめ お疲れ様でした！ 放物線のグラフを書くためには 丁寧に点を取って、それらをなめらかーに結ぶ！ これだけですね。 何度も練習すれば 誰にでも簡単に書けるようになります。 レッツ！ 練習 (/・ω・)/例：y=x, y=x, y={2^x} グラフの縮小率を大きくすると、広い範囲が見られます。逆に、縮小率を小さくすると、原点付近を拡大できます。 指数関数について y=x 2 ではなくて、y=2 x としてみます。 指数関数と対数関数は対の関係です。

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

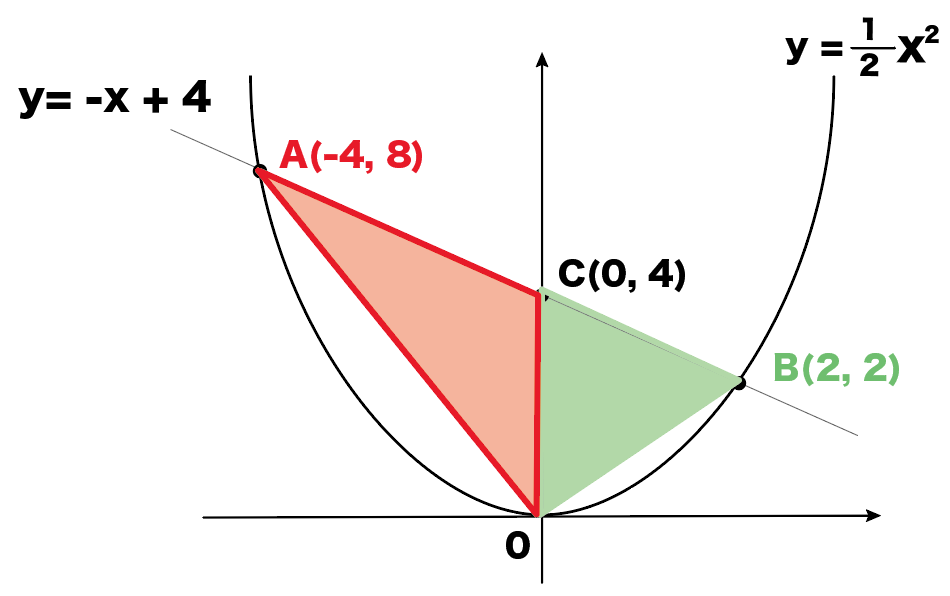
二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく

§1 2次関数 2．2次関数のグラフ(1) 2次関数のグラフは，放物線とも呼ばれ，ボールを遠投したとき描く曲線のような形をしています。その曲線を式で書くと，y=ax 2 (a≠0) の形に書かれます。 この章では，この曲線について，前の章で学んだ平行移動を行なうことにします。二次関数の接線は判別式を用いて求めることもできる。接線の方程式を y − (− 2) = m (x − 1) y(2)=m(x1) y − (− 2) = m (x − 1) とおくと，接線と二次関数の共有点は1つであるので，二次方程式 x 2 − 3 x = m x − m − 2 x^23x=mxm2 x 2 − 3 x = m x − m − 2 は重解を二次関数のグラフ③ 二次関数のグラフ③ 今度は y＝2x 2 のグラフについて考えてみよう。 y＝2x 2 のグラフをかくために、 x の値に対応する y の値 について考えよう。 x

数学教材 中間発表

数学 中3 35 二次関数のグラフ Youtube

のグラフは, a>0 の場合、右図のようになります。 a>0の場合、xの正負にかかわらず、yは常に正の値をとっています。 また、y軸に対し左右対称であることも分かります。 そして座標平面において、1次関数が直線、反比例関数が双曲線を描くのに対し、 移動前の点の y 座標（上の表の2段目）に 2 2 を加えたものが、新しいグラフ上の点の y 座標となります。 このことから、移動後のグラフに対応する新しい関数は y = x2 2 y = x 2 2 であることがわかります。 上の黒い太線のグラフが y = x2 2 y = x 2 2 のグラフということです。 グラフが二次関数y＝x2乗のグラフを平行移動したもので、点(1,4)を通り、x＝3のとき、最小値をとる二次関数は何か。教えて下さい。＞x＝3のとき、最小値をとる二次関数 y ＝ x^2 （「2乗」をこう書きます）は「下に凸」なので、「頂点

２次関数のグラフ

数学 ２次関数 頂点の求め方 オンライン無料塾 ターンナップ

定義：2次同次関数 、2次形式 ・「2変数x,yについての二次形式」「x,yの2次同次関数」とは、 2変数x,yについての多項式で、2次の項ばかりからなるもの すなわち、 Q (x,y) = ax 2 2 bxy c y 2 (a,b,cは定数) のことをいう。 ※詳細→2変数2次形式 文献

二次関数のグラフの書き方とグラフの問題を一気に紹介 スタディクラブ情報局

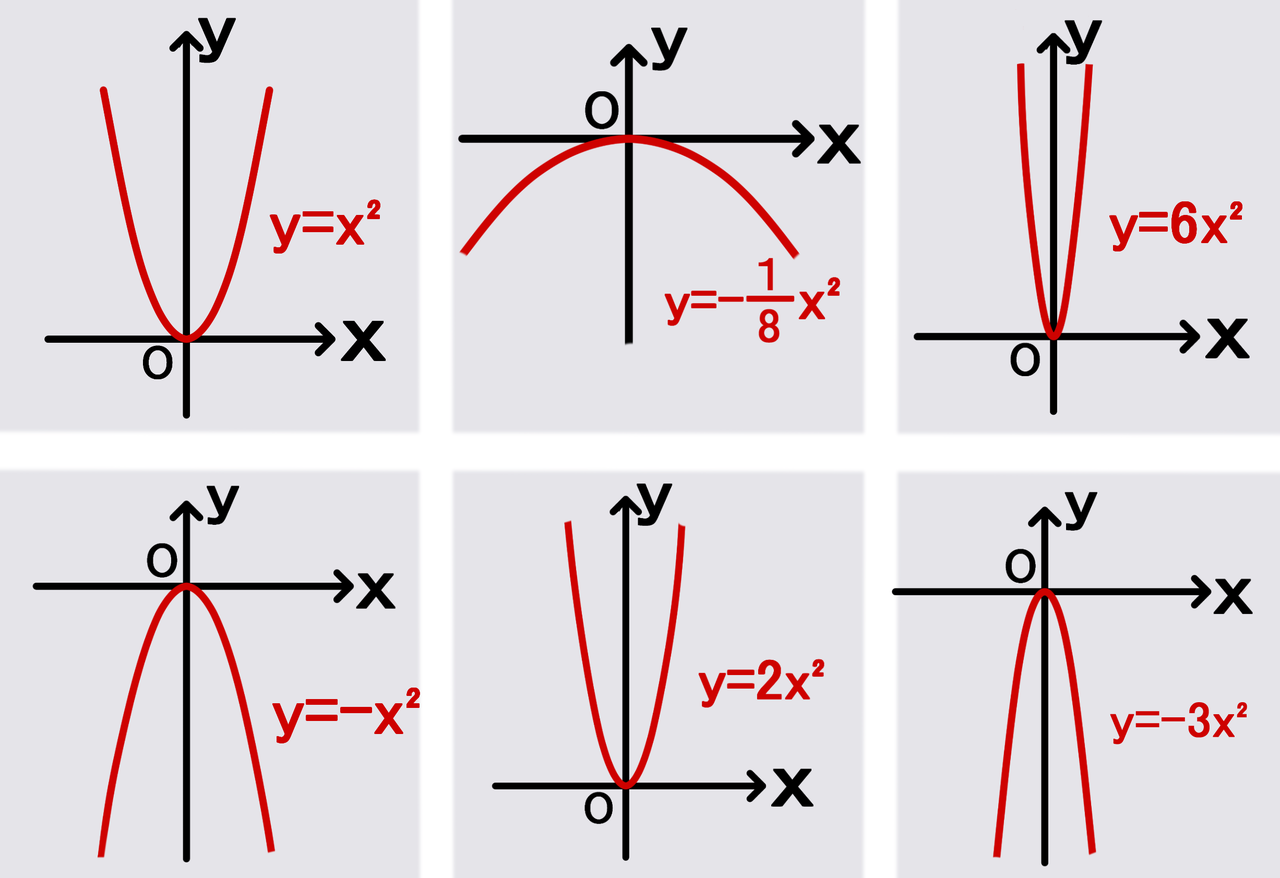
2次関数y Ax のグラフ 放物線 の形は 上に凸 下に凸の場合があるのだが バカでもわかる 中学数学

解説がわかりません なぜｙ ｘ２乗 3ｘを平行移動した放物線の二次関数はｙ ｘ２乗 Clear

２次関数 Y A X P のグラフの書き方 グラフの平行移動 数学i By ふぇるまー マナペディア

3

変化の割合 二次関数y Ax2の裏ワザ公式 どうやって解くの 数スタ

Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf

高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット

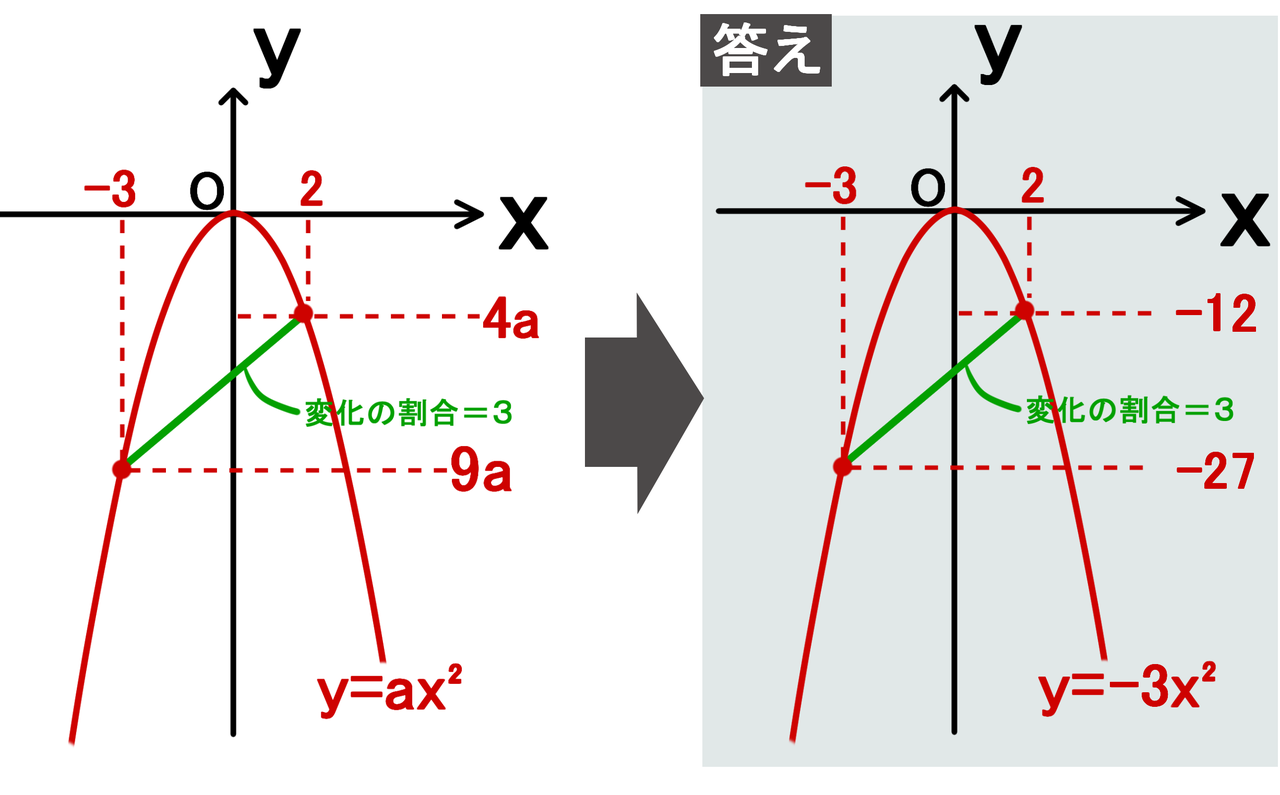
関数y Ax の 変化の割合 の問題 Xの値がaからa 2まで増加したときに Yの値は バカでもわかる 中学数学

１ の問題で関数y X２乗 1を平方完成をしないのは二次関数と書いてな Yahoo 知恵袋

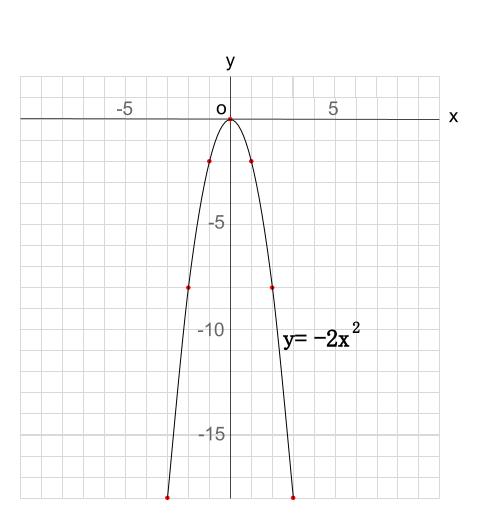
中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

授業実践記録

1

Aを実数の定数とする 二次関数y X 2 2ax A 2 1の0 X 2における最小値 高校 教えて Goo

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

2次関数のグラフと直線

二次関数の移動

二次関数のグラフ

高校数学 Y A X P 2 Qのグラフ2 練習編 映像授業のtry It トライイット

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

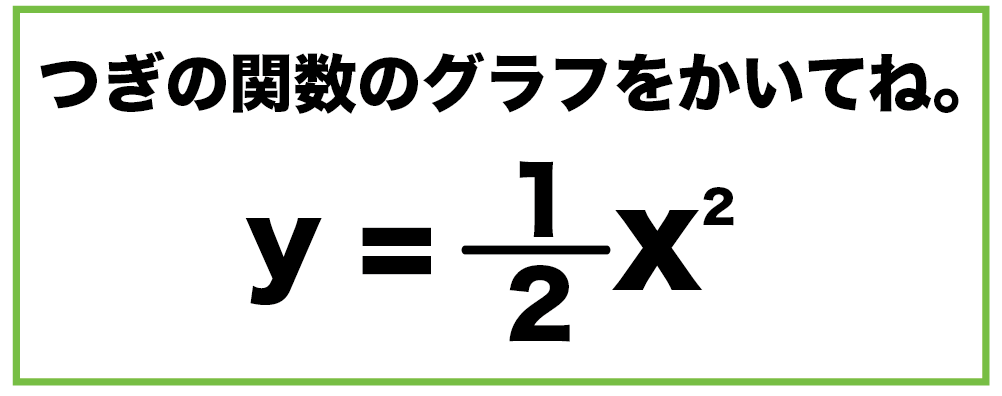
中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

基本 二次関数 Y Ax 2 のグラフ なかけんの数学ノート

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

中学数学 関数

Y X２乗 4x 1のグラフの書き方を教えてください グラフの画像をつけ Yahoo 知恵袋

授業実践記録

2次関数のグラフ 2次関数のグラフの式の 頂点の求め方を教えて下さい Okwave

２次関数のグラフと直線

2次関数 方程式 のグラフ もう一度やり直しの算数 数学

基本 指数関数のグラフ なかけんの数学ノート

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

Aは正の定数とする 関数y X 2 4x 3 0 X A の最大値を求めよ 解き 高校 教えて Goo

二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく

次の2次関数をy A X P 2乗 Qに変えてください Y X2乗 X Clear

２乗に比例するグラフ 中学から数学だいすき

二次関数のグラフ エクセル Excel エクセルの学校

中学数学の二次関数 問題の解き方の基本とグラフの書き方 リョースケ大学

基礎数学 4回目

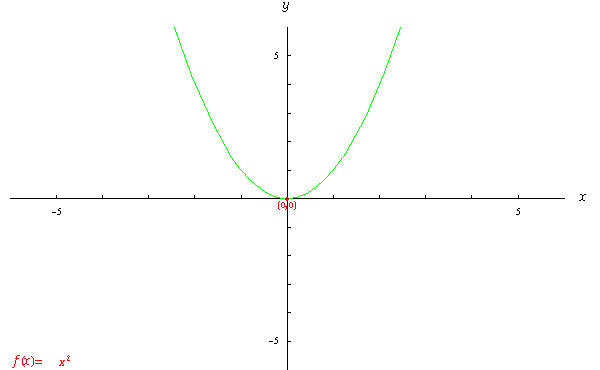
1変数関数y F X X 2の性質 数学についてのwebノート

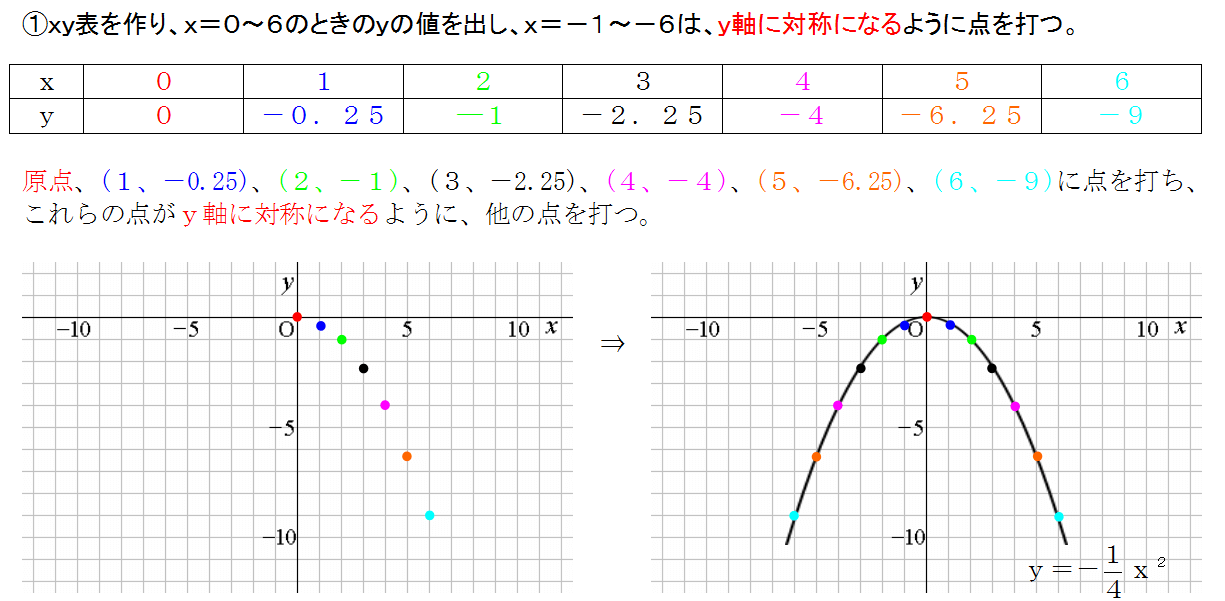
二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

1

二次関数の問題です 二次関数 Y 1 2xの2乗 2ax Aの2乗 4a 高校 教えて Goo

関数y X 2のグラフの性質 勉強ナビゲーター

Aは正の定数とする Clear

3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

Y 1 X2乗のグラフ Youtube

高校数学 2次関数がx軸から切り取る線分の長さ 受験の月

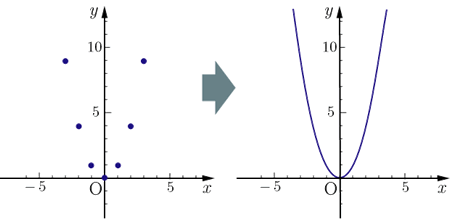
2次関数のグラフ Y X 2

2次関数とは 式とグラフの解説 数学fun

Yx2乗 ニスヌーピー 壁紙

ｙ ｘ２乗 2ｘ 2を平方完成したらどうなりますか 途中式教えてください Clear

1

Yx2乗 ニスヌーピー 壁紙

Y X 2 2x 1のグラフあってるでしょうか 解説のグラフと Yahoo 知恵袋

高校数学です 二次関数y X 6xのグラフを書け また その軸と頂点 高校 教えて Goo

2乗に比例する関数のグラフ 放物線 の書き方 無料で使える中学学習プリント

中学数学 関数

因数分解とグラフ 中学から数学だいすき

Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋

３次関数はどうなる 中学から数学だいすき

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

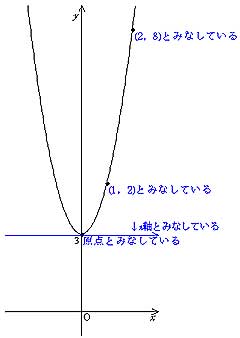
授業実践記録

2次関数y X2乗 2x 2 X 1 のグラフ 最大値 最小値 Yahoo 知恵袋

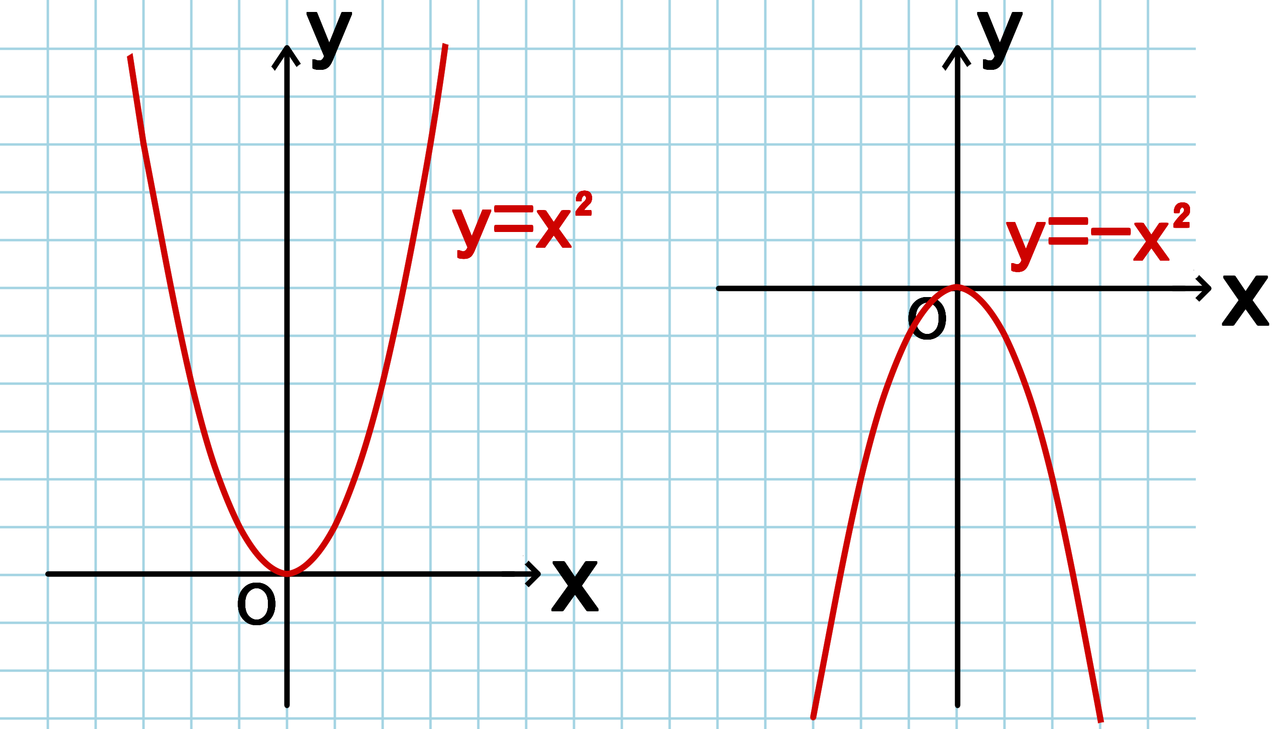
2次関数y Ax のグラフ 放物線 の形は 上に凸 下に凸の場合があるのだが バカでもわかる 中学数学

頂点が原点以外にある二次関数のグラフ 2 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

頂点が原点以外にある二次関数のグラフ 1 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信

無料でダウンロード 関数 Yx2乗 ニスヌーピー 壁紙

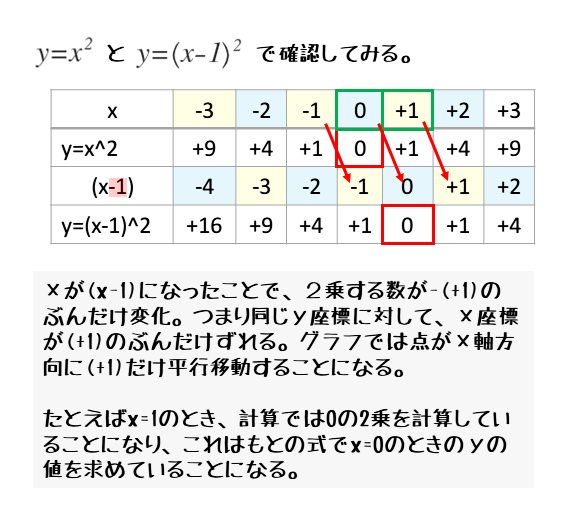
２次関数 ２次関数のグラフの平行移動について 日々是鍛錬 ひびこれたんれん

２次関数の各係数の意味

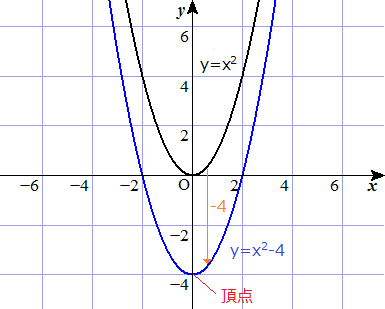
例題で学ぶ高校数学 Y Ax2 Q

2次関数のグラフ グラフの書き方 グラフの特徴 基 数学の解説と練習問題

２乗に比例するグラフ 中学から数学だいすき

Y Ax 2 Bx Cのグラフ 数学i フリー教材開発コミュニティ Ftext

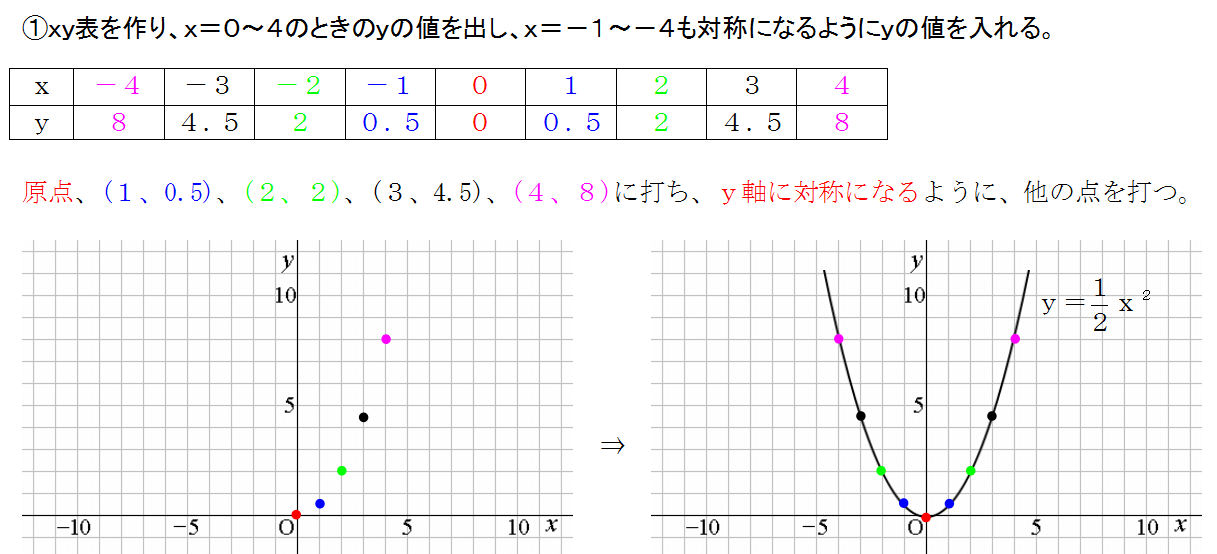
2乗に比例する関数 グラフ

二次関数のグラフの書き方 中学生の数学で非常に大切だ 三重の個人契約家庭教師

二次関数のグラフ

数学 ２次関数 頂点の求め方 オンライン無料塾 ターンナップ

中学数学 Y Ax 2 のグラフ 中学数学の無料オンライン学習サイトchu Su

高校数学 Y A X P 2のグラフ2 練習編 映像授業のtry It トライイット

二次関数の値の変化 Y X2 4x 5を 平方完成してグラフを書く 私 Yahoo 知恵袋

2次関数のグラフの書き方 頂点 平行移動について全て語った 理系ラボ

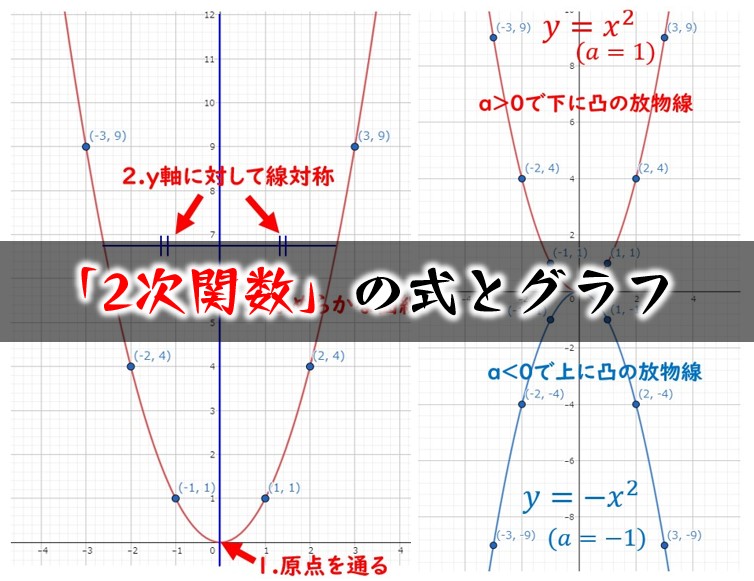
2次関数とは 式とグラフの解説 数学fun

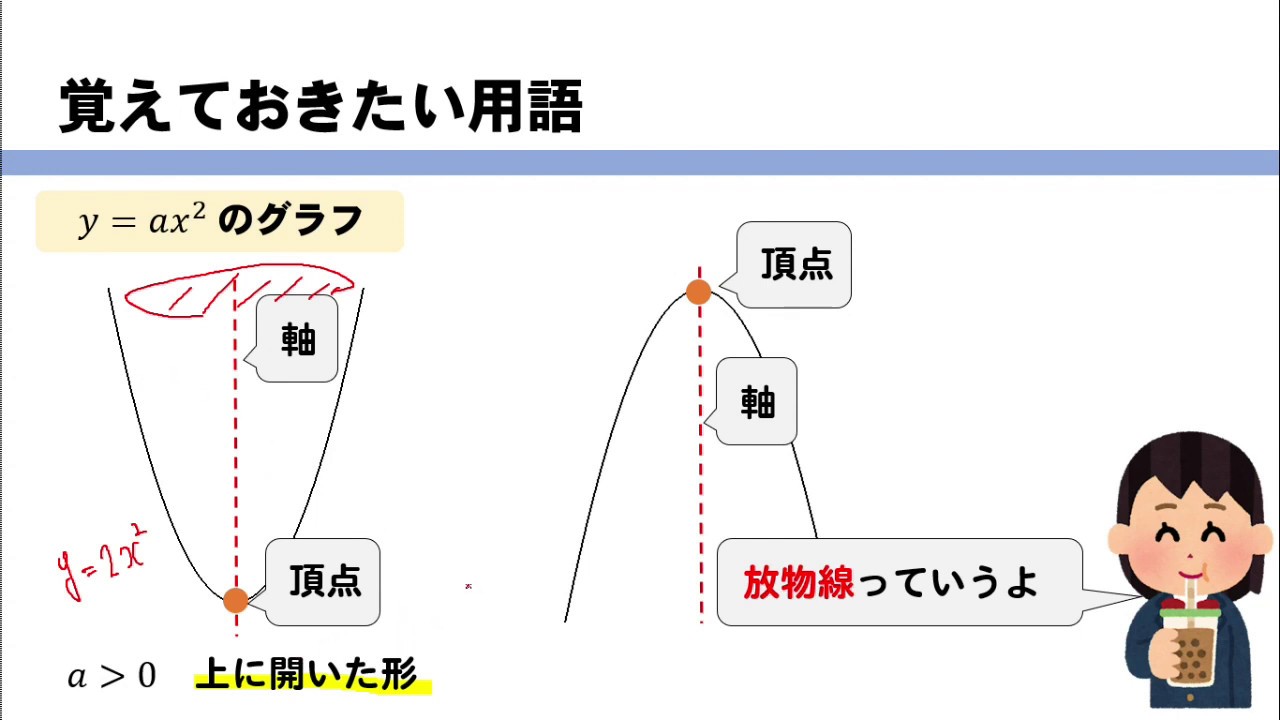
関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

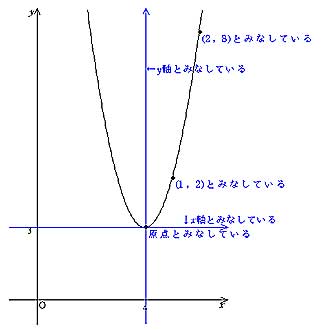
授業実践記録

Incoming Term: 二次関数 y=x2乗 グラフ,