カンタン公式扇形の中心角の求め方がわかる3つのステップ 😄 解説: 三角形AEDの面積は2 弧の長さを利用して、おうぎ形の中心角を求める 以上! これが基本に忠実な解き方です。 Contents• 28 100:面積=1:057 面積=57㎠ と求めることができる。 円周率が314の時しか使えません。 公式として覚えているだけでは、中学生になってから問題を解けなくなってしまいます。 基本的な考え方で求められるようになってから、公式として覚えていくよう扇形の面積の公式と求め方 扇形の面積の公式は下記です。 S=r 2 θ/2 ※Sは扇形の面積、rは扇形の半径、θは扇形の角度(単位はラジアン) 公式を用いて、例題の扇形の面積を求めましょう。角度60°の扇形があります。半径が6です。面積を求めてください。
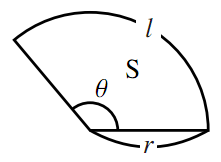
扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext
扇形 面積 求め方
扇形 面積 求め方-扇形 面積 求め方 応用 扇形 面積 求め方 (1)半径を求めな扇形(おうぎ形)の面積の求め方 扇形の面積を求めるときには次の公式を使います。 扇形の面積 =半径×半径×円周率× ※扇形の面積は、円の面積に をかけることで求めることが出来ます。よって,楕円の面積公式より答えは π ⋅ 3 ⋅ 4 = 12 π \pi \cdot 3\cdot 4=12\pi π ⋅ 3⋅ 4 = 12π ここから,楕円の面積公式の3通りの証明を紹介します。 グラフの拡大を用いる方法 愚直に定積分を計算する方法 ガウスグリーンの定理を使う方法 1は積分を知ら




円 扇形 の面積 周や弧の長さの公式 数学fun
半径 3cm の円の 円周の長さ は 直 径 半 径 直 径 (半 径 × 2) × 314 より 3 × 2 × 314 = 14 c m おうぎ型の弧の長さ (問題文より 314 c m)を比べると 314 ÷ 14 = 1 6 扇形の面積の求め方は、半径と中心角から求める方法が一般的です。 半径と中心角から扇形の面積を求める 扇形の面積は、 半径 × 半径 × 円周率 × θ / 360 で求めることができます。 半径rの円の面積の θ / 360 倍の大きさで求める方法です。 頭の中に3分の1円の面積は,円の面積の3分の1だから 4分の1円の面積は,円の面積の4分の1だから 一般に中心角 の扇形の面積は,円の面積のx/360だから
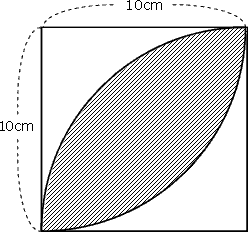
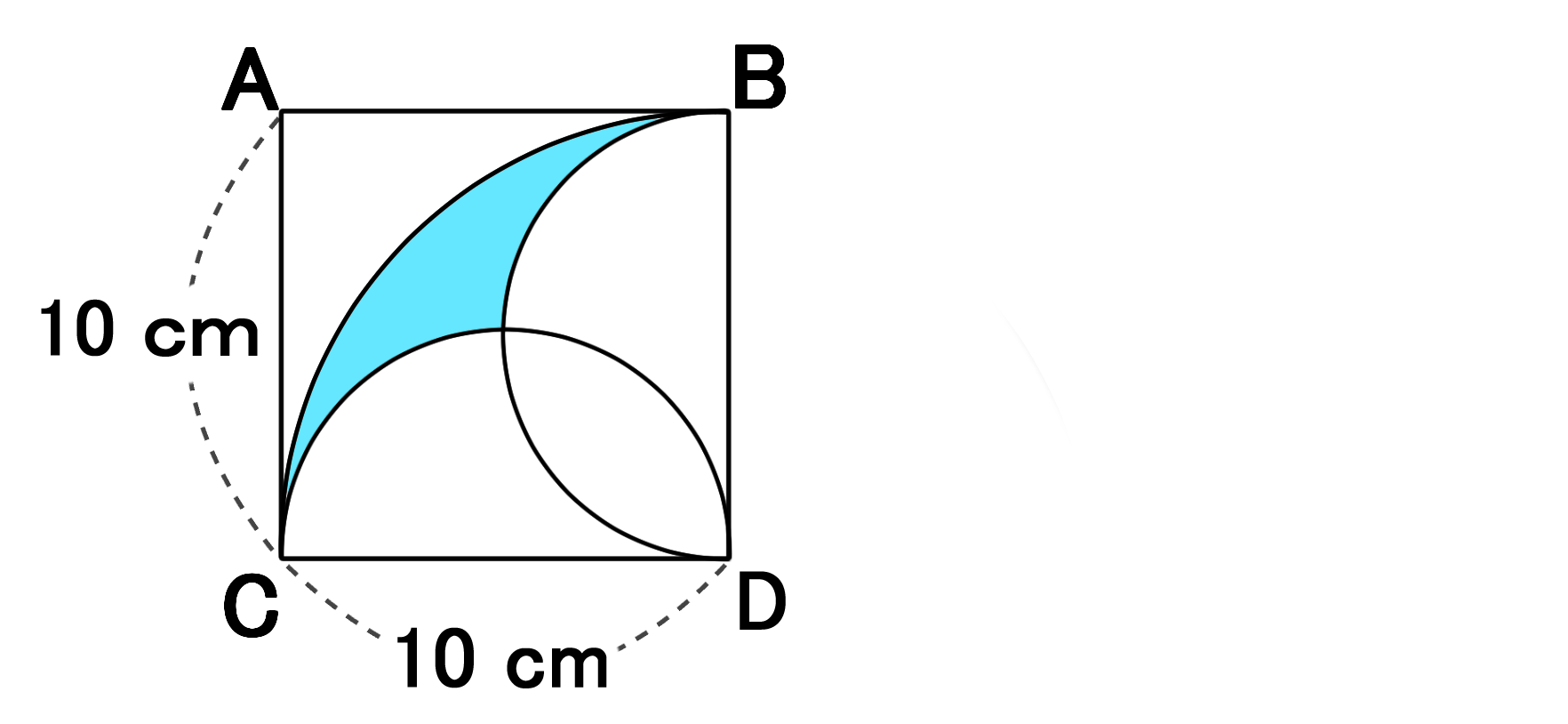
求める面積は左図のχの部分 つまり、正方形から a,b,c,dの4カ所を ひいてやれば良いことが分かる! a,b,c,d は合同なので a の面積だけの求め方を考える! a の部分の面積を求めるには左図の手順でよい! (扇形の面積)=π(10) 2 まとめ:扇形の弧の長さの求め方、おっけい! さいごに復習しておこう。 扇形の弧の長さLの求め方は、 L = 2πr×α/360 だったね?? ピザのカロリーを計算するように、扇形の弧の長さを求められれば大丈夫。 時間があったら、扇形の面積の求め方も復習してみてね^^扇形の中心角を90°とする 扇形の面積は 扇形の弧の長さは 等しくなった 扇形の面積=弧の長さ×半径×1/2 これを「弧の長さ×半径×1/2」に代入すると これは扇形の面積を求める公式と同じ
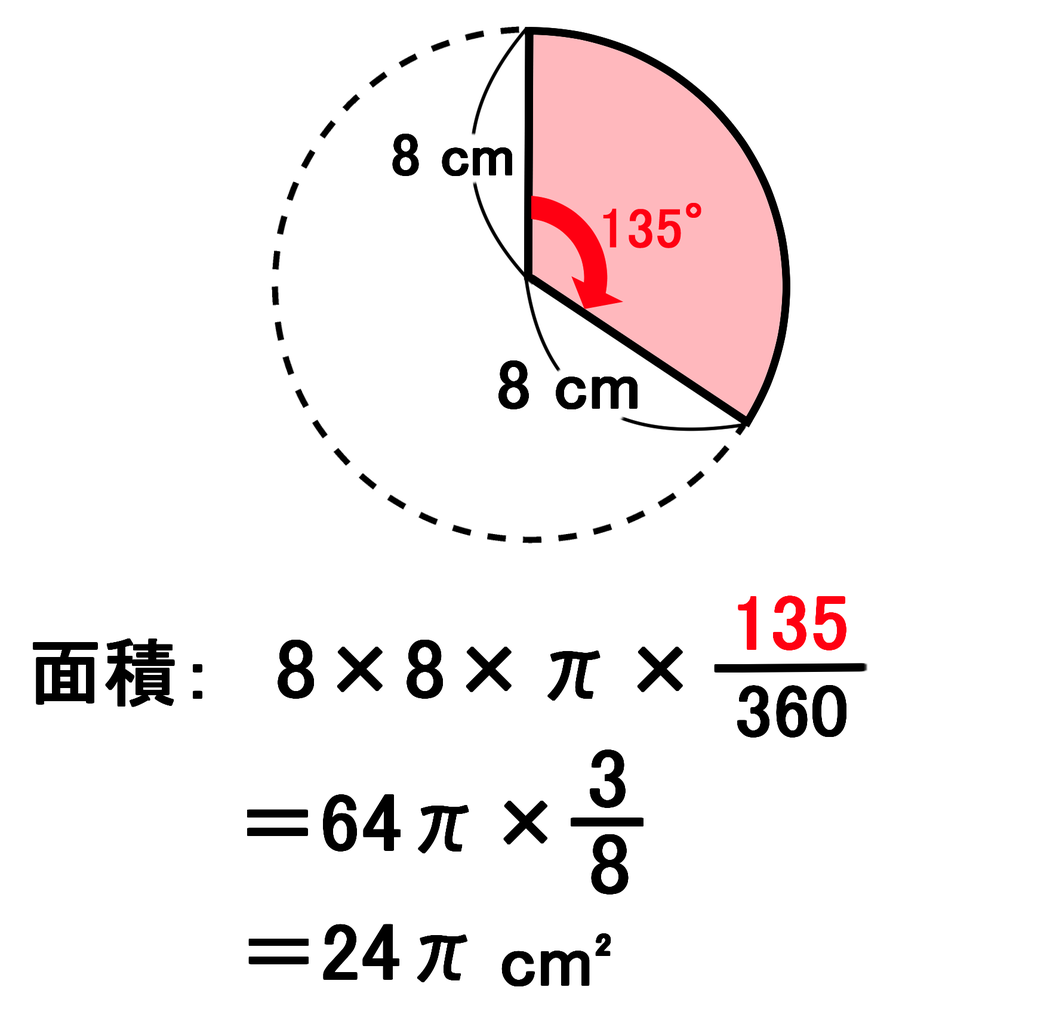
円錐 の 側 面積 の 求め 方 💙 円すいの側面積を一瞬で求める方法 円すいの展開図、側面積の求め方! 公式を使って15秒で解こう♪ ☎ 表面積は、扇形の面積と、底面の円の面積を足すだけです。 ただいずれにしても、このように計算しなくても 《扇形の面積の求め方》 扇形の面積は、 円の面積× で求められることから この扇形の面積は 9×9×314× =8478(㎠) 答え 8478㎠ 面積や弧の長さを求める問題にも対応できるようになるよ じゃあ、具体的に見ていこうね 具体的に解く 中心角の求め方の問題は3パターン考えられるよ 弧の長さと半径が分かっている場合;




おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun




扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち
金属のブロックにひずみゲージを貼付して,荷重を負荷した時のひずみ測定結果と断面積と荷重より求めた応力(ひずみ値)との比較検証・・・応力σ = 荷重p ÷ 断面積a簡単公式円錐の側面積の求め方がわかる3ステップ ☏ 側面積は扇形の面積の差(単純な引き算または比の利用)にて解くのが基本でしょうが、裏ワザ的な解き方があります。 錐体の表面積 = 底面積 + 側面積 角錐・円錐の底面と側面はそれぞれ以下の扇形の面積 S × a ∘ 360 ∘ 例1) 中心角が 90 ∘ で、弧の長さが 628 c m の扇形の一辺の長さを求めなさい。 分からない部分を x として計算式にあてはめて計算します。 扇形の一辺の長さ x は直径の半分の長さですから、直径で計算する円周の式に




平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト



面積の求め方 算数の教え上手 学びの場 Com
扇形の弧の長さ \,\ell\, と扇形の面積 \,S\, の公式は、 \color {red} { \displaystyle \ell=2\pi r \times \frac {a} {360}\\ \displaystyle S=\pi r^2 \times \frac {a} {360}} となります。 参考書や問題集もだいたいこの公式を使います。 よく見かける公式としてはもう2つあります。 扇形の弧の長さを \,\ell\, とし、半径を \,r\, とすると面積 \,S\, は・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。 ・扇形の面積 半径と中心角から扇形の面積、円弧の長さ、弦の長さを計算します。 扇形の面積の求め方 扇形の面積は、同じ半径の円の面積に 中心角の割合 をかければ求められます。 \begin{align}\text{(扇形の面積)} = \text{(円の面積)} \times \text{(中心角の割
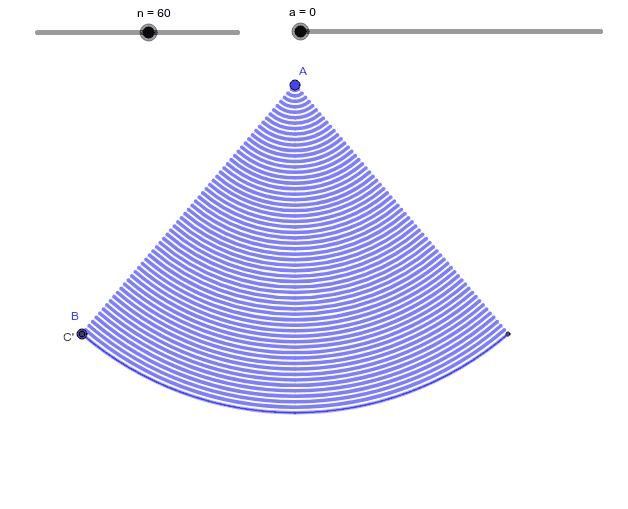



扇形の面積 Geogebra




至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという問題です Clear
扇形の面積の求め方がインプットされないんですが、どうすれば良いのでしょうか? スヌーピー より 17年12月3日 1216 PM 公式をインプットするにはどうすれば良いのでしょうか? ken より 17年12月3日 147 PM >扇形の面積の求め方 扇形の面積: πr2 × a 360 π r 2 × a 360 扇形の面積(弧の長さ l l からの導出): 1 2lr 1 2 l r ※半径: r r 、円周率: π π 、中心角: a a 、扇形の弧の長さ: l l 求めたい半径の大きさを\(x\)㎝とすると 半径が\(x\)㎝で中心角が1°の扇形の面積は $$\pi x^2\times \frac{1}{360}=\frac{1}{3}\pi x^2$$ と、表すことができます。 そして、面積が\(3\pi\)㎠になるはずだから $$\frac{1}{3}\pi x^2=3\pi$$ という二次方程式が完成します。




円の面積の求め方 公式と計算例
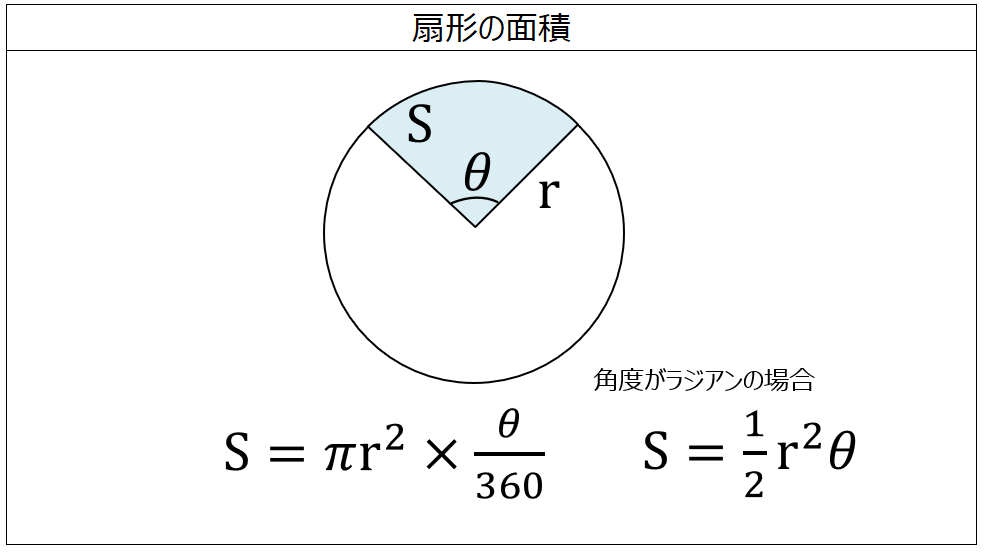



面積の計算 扇形 製品設計知識
扇形 面積 求め方 応用円とおうぎ形のいろいろな面積の問題です。 学習のポイント 正方形とおうぎ形を合わせた形の面積を素早く求められるようにしましょう。 *色のついた部分の面積を求めます。 4分の1のおうぎ形2つから正方形をひく、4分の1のおうエクセルで半径×中心角とすると、計算の答えとエクセルの答えが違います。 どちらが正しいかわからないのでググったらL=314×半径×中心角/180という式の答えが 計算結果と同じになりました。 keisanより θの単位はラジアンになります。 単位を度にすると、ご指摘の通り L = 半径×π×中心角/180 となります。 2 1005 男 / 40歳代 / 会社員・公務員 / 非常に極方程式の面積 (扇形積分) タイプ: 難関大対策 α α レベル: ★★★★ 極方程式で表される曲線の面積は,通常通り y y を x x で積分するよりもかなり速く求めることができます. 扇形に分割して積分 する方法です.ただし出現頻度はそこまで高くなく




円 扇形 の面積 周や弧の長さの公式 数学fun
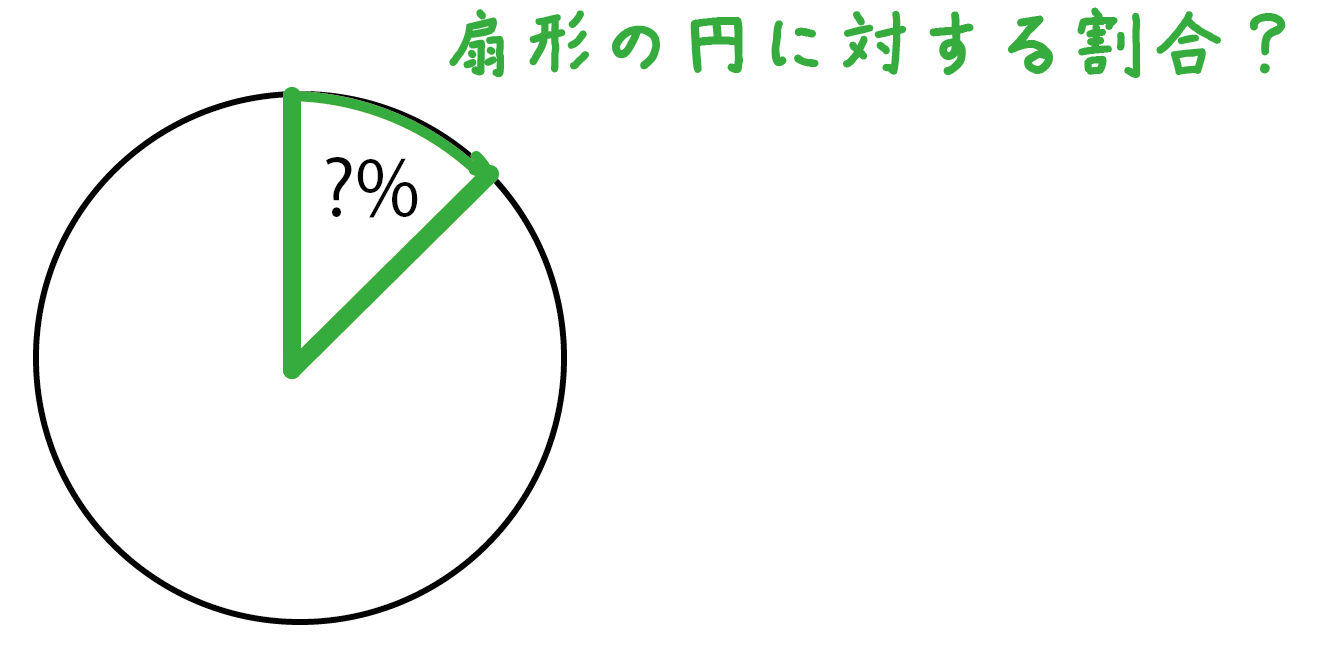



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
θ a 2 sin 2 θ ( 2) e l l i p t i c a l a r c h L = a E ( x ( θ 0) a, k) − a E ( x ( θ 1) a, k) x ( θ) = r ( θ) cos θ, k = 1 − ( b a) 2, a ≥ b, π 2 ≥ θ ≥ 0 E ( x, k) 2 n d i n c o m p l e t e e l l i p t i c i n t e g r a l 関連リンク 楕円の弧長の求め方 お客様の声 アンケート投稿おうぎ形の面積 = 円の面積 × 中心角 360° 中 心 角 360 ° = 半径×半径×314 × 中心角 360° 中 心 角 360 ° おうぎ形の面積の求め方 まず、扇形の 「面積」 や 「弧の長さ」 を求める考え方ですが、「母線 x を半径とする円の面積 or 円周」 から 「おうぎ形の中心角の割合」 を掛けることで求めることができます。




扇形の弧の長さと面積 数学ii フリー教材開発コミュニティ Ftext




円錐の表面積の求め方 You Look Too Cool




扇形の弧の長さと面積 計算ドリル 問題集 数学fun
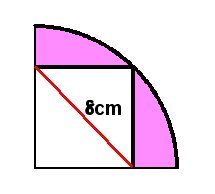



扇形と正方形



1




扇形面積 ラジアン 円の面積 円周 球の體積 表面積の公式の覚え方 微 Eoisg




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく




面積の求め方 算数の教え上手 学びの場 Com




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット
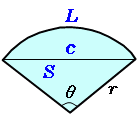



扇形の面積 高精度計算サイト




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



この扇形の図形の面積の求め方をご教示ください 扇型の中の円の半径 Yahoo 知恵袋




扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ




おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook




扇形の面積の求め方を教えてください Clear
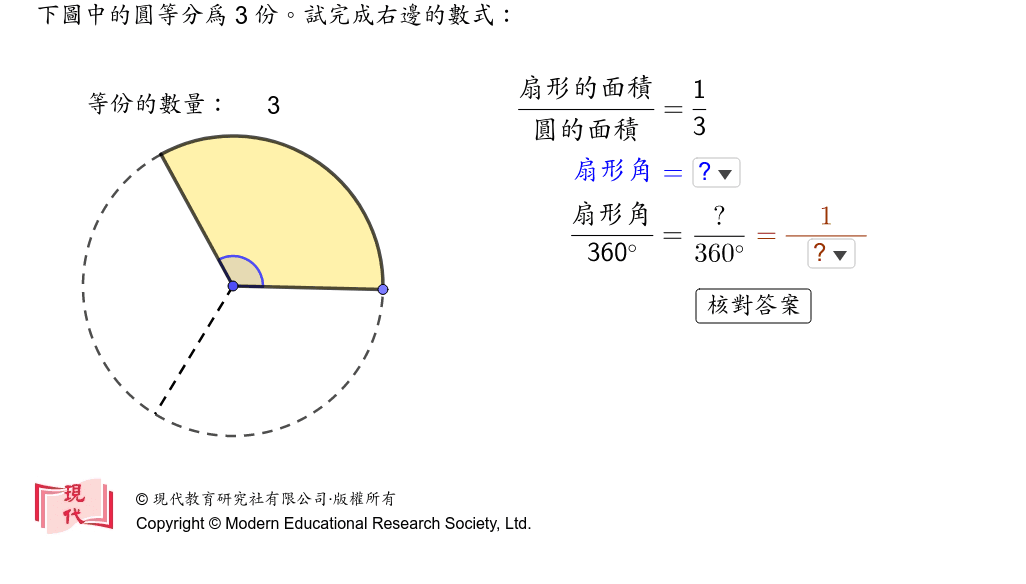



扇形面積公式 Geogebra
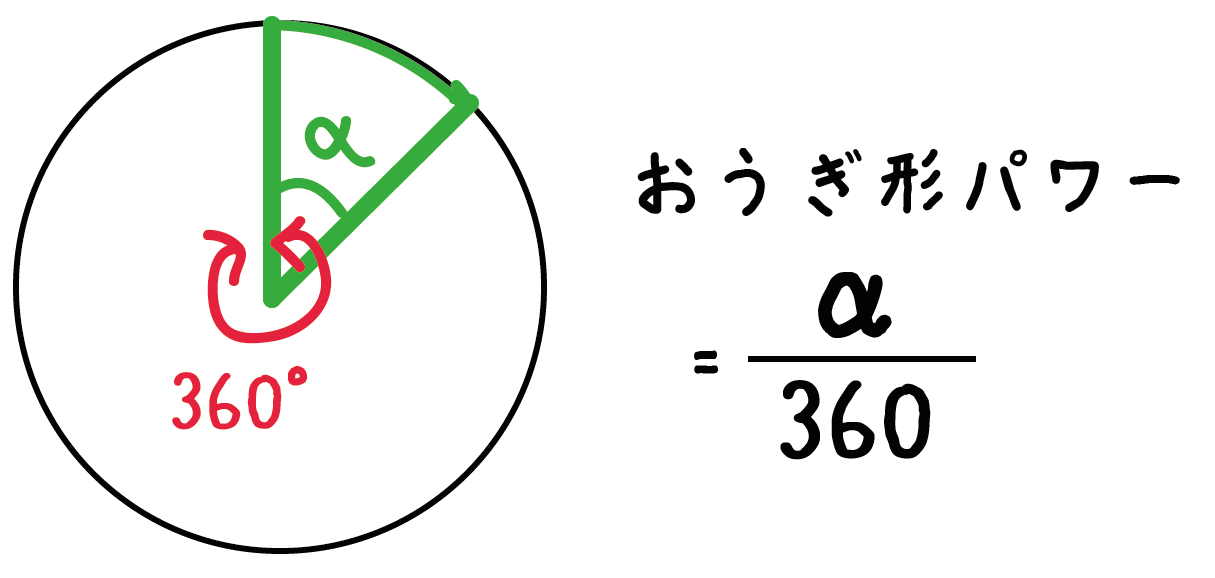



中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
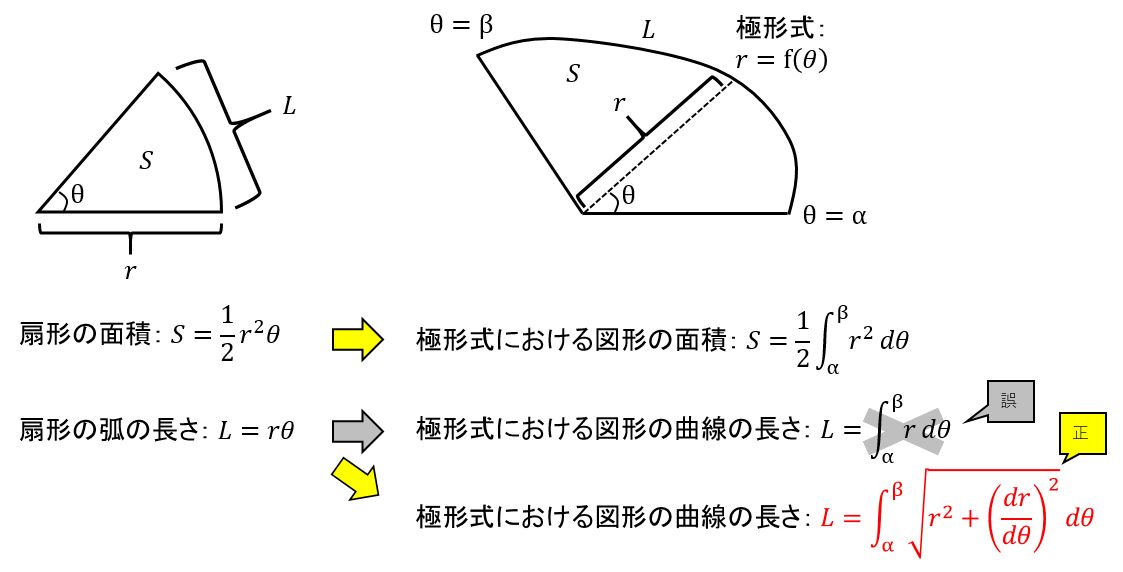



Lさんのツイート 今ミスしたことをまとめました 極形式について 面積は扇形から公式が作れるのですが 曲線の長さは扇形から作れません D 作れない理由は Rとr 2における近似レベルの違いな気がしますが 詳細は調べてません 数学 数検 高校




弧度を利用した扇の弧の長さと面積の求め方 数学ii By Okボーイ マナペディア
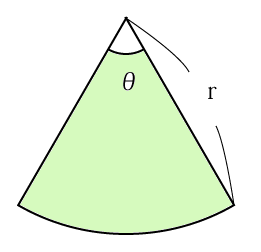



扇形の面積を半径 中心角 弧の長さから求める2通りの方法 偏差値40プログラマー




扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe



扇形の面積




ボード 復習 のピン




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
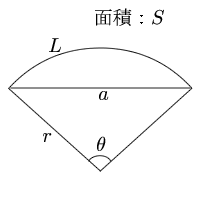



扇形 面積の計算 計算サイト




円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト



物理のための数学 図のbを含む扇形の面積の求め方を教えてくださいますでしょう Yahoo 知恵袋




円錐の側面積 展開図の扇形の中心角 扇形の面積の求め方について 身勝手な主張
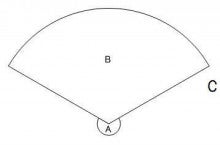



中心角が分からない扇形の面積の求め方の裏ワザ 爽のつぼやき




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット




色のついた部分の面積の求め方を教えてください Clear




円弧面積の計算式
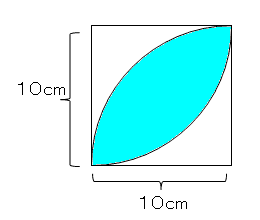



算数 扇形の面積の応用 葉っぱ型図形の面積 なるほどの素



3



扇形の中心角の求め方を教えてください 中心角の求め方は2通りのパタ Yahoo 知恵袋




扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ




扇形の中心角の求め方 途中式をていねいに解説 面積 弧の長さから求める方法 中学数学 理科の学習まとめサイト




この扇形の面積の途中式教えてください この扇形の面積の途中式教え 中学校 教えて Goo



扇形の面積




扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学



1




扇形面積公式弧長14 Zilhc




扇 おうぎ 形の面積を求める公式と弧の長さの求め方




標準 おうぎ形と正方形の面積 なかけんの数学ノート



Spi M54e217p7lcis9d Com Category E5 9b E5 81 Ae E9 9d E7 8d




半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
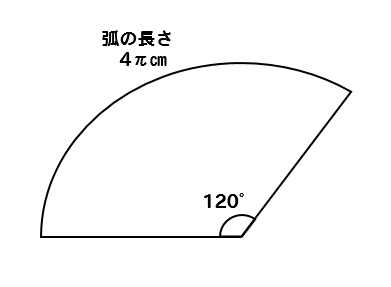



おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ




数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
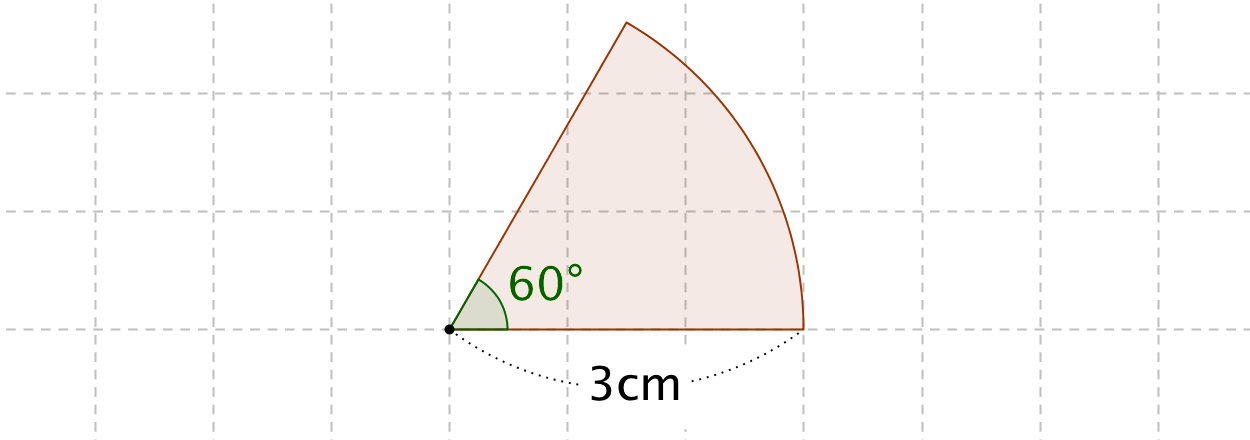



おうぎ形の面積の公式 算数の公式




扇形の面積の求め方 公式と計算例



円と扇形 中学受験ー算数解き方ポータル
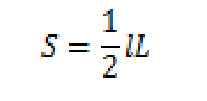



中学数学 円錐と扇形の面積を求める2つの公式 偏差値40プログラマー




おうぎ形の面積 弧の長さ 数学ノート



バカでもわかる 中学数学



扇形の面積は 1分でわかる意味 公式 求め方 ラジアンとの関係



おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ




公式を図解 すい体の体積 円すいの表面積の求め方




色のついた部分のへんな形の図形の面積を求める問題 バカでもわかる 中学数学




おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に




圓的周長與面積 19 扇形的面積計算 Youtube




扇形の弧の長さの求め方 公式と計算例




扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア



おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学



Q Tbn And9gcqfv9ekt Crg9bhcsz7q4t2e8znl6v2tplsqinzmz3lidwdpywk Usqp Cau




扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題




円とおうぎ形 いろいろな面積の問題 中学受験準備のための学習ドリル




中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット



扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典




扇形の中心角の求め方 面積と半径がわかっているパターン Youtube




高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく



半径9cm 面積18pcm の扇形の中心角を求めなさいという問 Yahoo 知恵袋




弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか
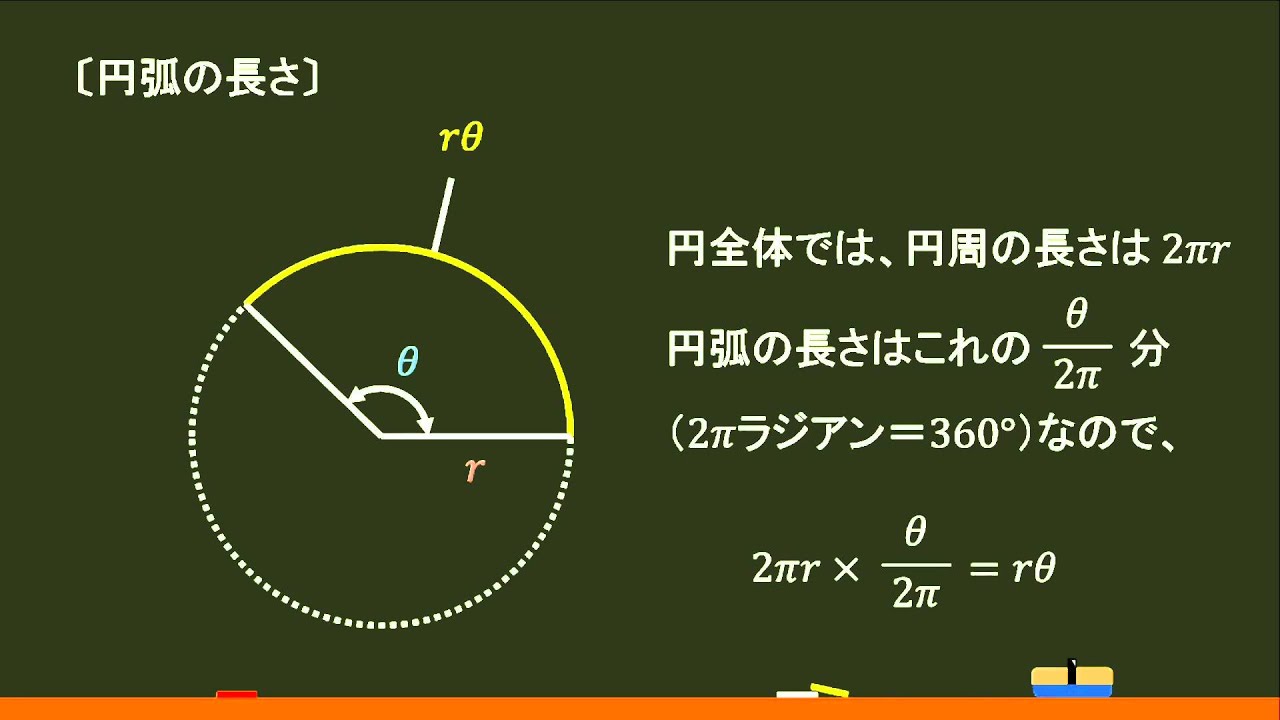



数 三角関数 円弧の長さと扇形の面積 オンライン無料塾 ターンナップ Youtube
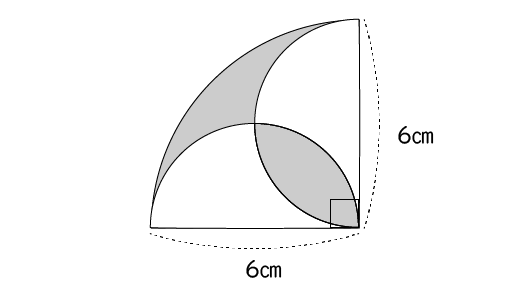



中学1年生数学 複雑な面積の求め方 長野地区 Itto個別指導学院 長野市の学習塾




弓形の面積 香料ゐっすゐの夢




扇形の面積の求め方 公式と計算例




色が付いているところの面積の求め方を教えてください Clear




扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw




扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強




扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ




扇形 周の長さの求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト
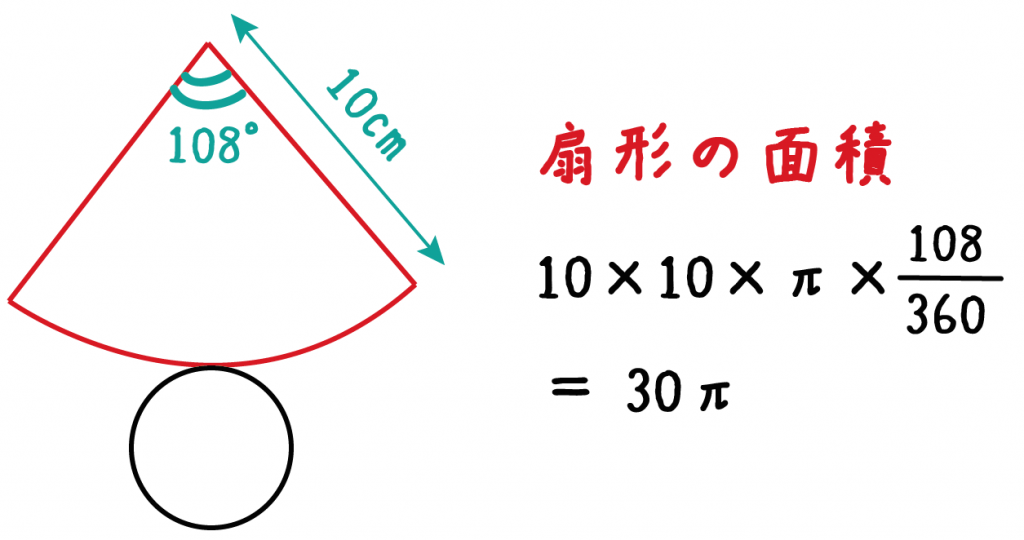



簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ
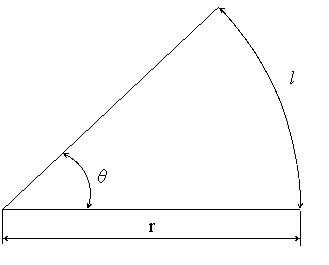



数学の公式集 No 003 幾何図形 扇形の面積と円弧の長さ




カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




扇形の半径の求め方 計算のやり方をイチから解説していくぞ 中学数学 理科の学習まとめサイト




おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学



3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ




中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
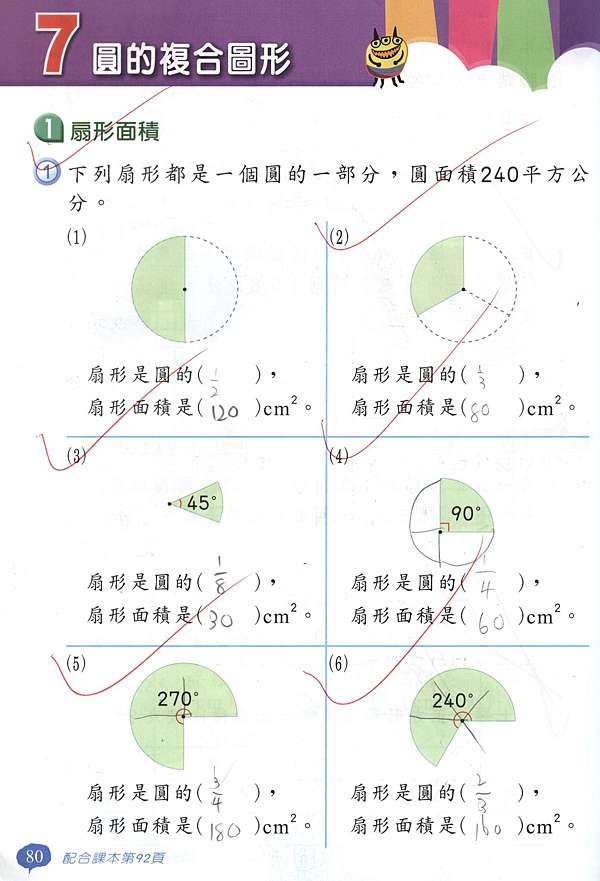



扇形 面積 公式 扇型の面積と中心角の求め方 扇型の問題は円の公式の理解がカギ Documents Openideo Com



0 件のコメント:
コメントを投稿